Notre cher Math Hatter répond à trois questions sur la pandémie Covid-19: les modèles mathématiques pour les faux positifs, la distanciation sociale en cours, le grand mathématicien britannique John Conway.
Le nombre inhabituellement important d’appels reçus par la permanence téléphonique 1-800-MATHATTER a, pour moi, au moins deux explications possibles. Tout d’abord, il me semble tout à fait naturel que la plupart d’entre vous, n’ayant pas d’autre choix que de rester à la maison, s’adonne à leur passe-temps favori : apprendre et faire des mathématiques ou bien regarder en boucle des vidéos de la formidable chaîne You Tube 3Blue1Brown. Ceux-là n’ont pas tant besoin d’aide que de conseils sur des livres ou autres vidéos. Parmi les autres, il y en a certains qui peinent parfois à comprendre toutes les subtilités des notions mathématiques abordés par les media à propos de la pandémie : aplanir la courbe, faux négatifs ou encore distanciation sociale.
“Cher Math Hatter, dit ainsi un élève de 3e, j’entends souvent parler de la croissance exponentielle mais je ne suis pas sûr de bien comprendre ce dont il s’agit. Pouvez-vous m’aider ? Merci. »
Je donnerai une réponse rapide, le sujet a déjà été abordé dans une précédente chronique qui est toujours disponible ici.
Et maintenant c’est un élève de CM1 curieux qui demande « Pourquoi est-ce que tout le monde parle de John Conway en ce moment ? »
Peut-être pas « tout le monde » mais c’est vrai que plusieurs réseaux d’informations ont évoqué la mort, le 11 avril, à la suite de complications liées au virus, du célèbre mathématicien britannique. Ayant enseigné à Cambridge puis à Princeton, John H. Conway est réputé dans le milieu des mathématiciens pour ses contributions diverses à plusieurs domaines tels que la théorie des jeux ou la topologie. Pour le grand public, il restera avant tout l’inventeur du « Jeu de la Vie », un jeu créé en 1970 et devenu un exemple de comment la complexité peut naître d’éléments simples. Le jeu a des connections avec les machines de Turing et les débuts de l’informatique mais ses règles sont vraiment très simples et ne nécessitent rien d’autre que du papier, un crayon et…beaucoup de patience. Si cela vous tente, vous pouvez trouver les instructions ici.
Poursuivons. Voici une question d’un enseignant du primaire :
« Cher Math Hatter, j’espère que tes rencontres zoom se passent bien. Je ne comprends pas pourquoi des tests qui ont une efficacité de 90 ou 95% peuvent donner autant de faux positifs. Merci. »
C’est une excellente question et pour y répondre complètement il serait sans doute nécessaire d’expliquer la notion de probabilité conditionnelle qui est au programme de Terminale. Au lieu de ça, quelques exemples devraient suffire. La première chose qu’il faut comprendre est la signification exacte de « efficacité de 90% ». Prenons un test de grossesse dont l’efficacité annoncée est souvent supérieure à 99%. Comment cela est-il mesuré ? C’est très simple. Le test est donné à des femmes qui savent qu’elles sont enceintes et on mesure le nombre de résultats positifs. Si, parmi 1000 femmes enceintes, 995 tests sont positifs alors le laboratoire dit que le test est efficace à 99,5%. Le problème, évidemment, c’est que les femmes qui utilisent un test ne savent pas si elles sont enceintes, elles doivent déduire d’un test positif qu’elles le sont. Cette différence qui peut sembler peu importante est en fait au cœur du problème.
Imaginons une maladie rare touchant une personne sur 10 000 dans la population et imaginons une ville d’1 million d’habitants. Cela signifie que 100 personnes ont la maladie. Si le test est efficace à 90% et que l’on teste ces 100 malades, 90 seront positifs. Les 10 autres sont des faux négatifs parce que le test dit qu’ils ne sont pas malades alors qu’ils le sont. C’est ce nombre-là qui doit être le plus faible possible.
Disons que le test est aussi efficace à 90% quand une personne saine est testée. Comme la maladie est rare, le nombre de personnes saines est très élevé, 999 900 exactement. Pour 10% d’entre eux, ou 99 990, le résultat du test sera incorrect. Ce sont les faux positifs et même s’ils représentent un danger moindre que les faux négatifs, les patients concernés peuvent, selon la maladie, commencer un traitement plus ou moins lourd pour de mauvaises raisons. Voilà un tableau résumant ce premier exemple :
| Malade | Sain | Total | |
| Positif | 90 | 99,990 | 100,080 |
| Négatif | 10 | 899,910 | 899,920 |
| Total | 100 | 999,900 | 1,000,000 |
Nous pouvons maintenant retourner le point de vue et répondre à la question suivante : si mon test est positif, comment savoir si je suis malade (un vrai positif) ou non (un faux positif) ? Dans ce premier exemple la réponse est sans appel puisque parmi les 100 080 qui ont un test positif (90+99 990) seulement 90 sont malades. Autrement dit, si un test est positif il y a à peu près 1 chance sur 1000 que la personne soit malade. D’une certaine façon, c’est cela la vraie efficacité du test et il y a au moins deux raisons expliquant pourquoi ce nombre est si faible. D’abord, la maladie est très rare et ensuite 90% d’efficacité n’est pas si élevé. Si on change ces valeurs en prenant une maladie touchant 1 personne sur 100 et une efficacité de 99% on obtient ce nouveau tableau :
| Malade | Sain | Total | |
| Positif | 9,900 | 9,900 | 19,800 |
| Négatif | 100 | 980,100 | 980,200 |
| Total | 10,000 | 990,000 | 1,000,000 |
C’est beaucoup mieux mais une personne dont le test est positif a toujours seulement une chance sur deux d’être malade. Tirer à pile ou face donnerait le même résultat. Les laboratoires savent très bien cela et parient sur le fait que la plupart des gens ne comprennent pas la différence entre la probabilité que le test soit positif si une personne est malade (l’efficacité qu’ils peuvent annoncer) et la probabilité que la personne soit malade si le test est positif.
Bien sûr, comme le coronavirus est contagieux, on peut s’attendre à ce que plus de personne soient atteintes au point qu’on ne puisse pas le considérer comme une maladie rare. Prenons donc les résultats d’une étude récente estimant que 20% des Newyorkais ont ou ont eu la maladie et une population de 10 millions pour rendre les calculs plus simples. Avec une efficacité de 99% on obtient les nouveaux résultats suivants :
| Malade | Sain | Total | |
| Positif | 1,980,000 | 800,000 | 2,780,000 |
| Négatif | 20,000 | 7,200,000 | 7,220,000 |
| Total | 2,000,000 | 8,000,000 | 10,000,000 |
On peut voir que 70% des gens dont le test est positif sont vraiment malades, notre meilleur résultat pour l’instant. Cependant, nous avons dans ce cas 20 000 malades qui pensent qu’ils sont sains et peuvent donc transmettre le virus. Comment faire mieux ? Peut-être avez-vous entendu parler de l’idée « d’immunité collective » disant qu’il est nécessaire que 70% de la population aient contracté le virus pour pouvoir dire que la pandémie est sous contrôle. Voyons les résultats que cela donne :
| Malade | Sain | Total | |
| Positif | 6,930,000 | 30,000 | 6,960,000 |
| Négatif | 70,000 | 2,970,000 | 3,040,000 |
| Total | 7,000,000 | 3,000,000 | 10,000,000 |
Bien sûr, il y a encore un grand nombre de faux positifs mais cette fois-ci plus de 99% des personnes dont le test est positif sont bien malades. Ça y est ! Nous avons atteint le 99% d’efficacité dans les deux sens. Ce résultat n’est pas très surprenant vu le nombre de gens malades.
Au final, on est face à une sorte de situation « catch 22 ». Si on a un test très efficace et beaucoup de malades, alors il y aura beaucoup de tests positifs mais il est impossible de savoir si plusieurs personnes sont malades sans faire beaucoup de tests. C’est pour cette raison qu’une affirmation gouvernementale du type « Nous ne sommes pas dans la situation de ce pays. Nous n’avons pas besoin de mettre en place une grande campagne de tests parce que nous avons peu de cas. » n’a pas beaucoup de sens car la raison pour laquelle ce pays sait qu’ils ont beaucoup de cas est parce qu’ils ont fait beaucoup de tests. Si vous n’ouvrez pas la porte, vous pouvez continuer à croire à l’illusion que votre maison n’est pas en feu, malgré la chaleur croissante et la fumée qui s’accumule…
La dernière question que je traiterai vient d’un parent : « Cher Math Hatter, Mme Estey a récemment évoqué une reprise hybride à la rentrée de septembre les élèves alternant les jours de présence pour respecter la distanciation sociale. Quel serait le meilleur moyen de disposer les tables dans une salle de classe si on veut avoir un maximum d’élèves ? Merci. »
C’est ma question préférée. La réponse n’est pas aussi contre-intuitive que la précédente mais elle possède une belle solution géométrique. Évidemment, on ne parle pas ici d’élèves dans une file d’attente souhaitant entrer dans la cafeteria. Ce problème est simple, chacun se tient 2 mètres derrière les autres.
En revanche, si on considère un groupe de personnes participant à un évènement dans un espace limité il faut les placer en formant des lignes et des colonnes. Si vous cherchez des photos de distanciation sociale sur internet vous trouverez certainement deux types d’arrangement : le carré et le triangle. Par exemple, j’ai trouvé une photo de centaines de Musulmans dans une mosquée indonésienne, debout aux intersections de rangées verticales et horizontales. C’est le carré. Cela semble naturel parce que les quatre côtés d’un carré ont la même longueur, 2 mètres chacun dans notre situation. Cependant, dans un tel carré, deux personnes situées aux extrémités d’une diagonale sont à une distance supérieure à 2 mètres, environ 2,83 pour être précis. (#CeBonVieuxPythagore)
Une autre photo montre un groupe de travailleurs d’une compagnie de livraison thaïlandaise attendant les commandes. Leurs chaises forment également des rangées mais cette fois une rangée sur deux est décalée de 1 mètre. C’est le triangle, que certaines personnes préfèrent peut-être appeler l’hexagone. Cette disposition peut sembler moins intuitive mais elle en fait très naturelle. Les pavages hexagonaux sont fréquents dans la nature et souvent utilisés dans l’art de la mosaïque. (Si vous voulez en savoir plus sur les pavages, vous pouvez lire cette chronique publiée il y a environ un an et disponible ici.) La raison est simple : si vous asseyez une personne à un endroit, la restriction des 2 mètres forme un cercle et vous pouvez asseoir 6 autres personnes sur ce cercle, tous à 2 mètres de leurs voisins les plus proches. Dans ce cas, chaque personne est entourée de 6 voisins tous situés à la distance de sécurité l’un de l’autre. Avec la formation en carrés, une personne est entourée par 8 autres, 4 à 2 m et 4 autres à 2,83 m.
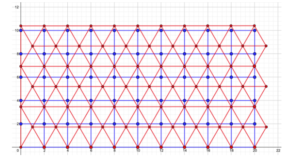Pour montrer cela avec une approche plus visuelle, considérons la figure ici qui illustre les deux dispositions superposées à l’intérieure d’un rectangle de dimensions approximatives 21 et 11 mètres. Un dénombrement rapide montre que 77 personnes peuvent s’asseoir dans la configuration en triangles (ce sont les points rouges) contre seulement 66 en utilisant les carrés (ce sont les points bleus, en n’oubliant pas que les points de la ligne du bas sont bicolores). C’est une différence de 11. Je sais que certains vont critiquer en disant qu’il y a 14 points rouges en dehors du rectangle formé par les points bleus mais ce rectangle n’est pas forcément l’espace considéré car il n’y a aucune raison que ses dimensions soient des multiples de 2 mètres. Par exemple, si les dimensions sont 9 et 19 mètres on obtient 60 points rouges et 50 bleus.
Ce résultat peut être montré de deux autres façons. Tout d’abord, on peut voir que la distance entre deux rangs de la disposition triangulaire n’est pas 2 mètres, mais environ 1,7 – la valeur exacte est en fait la racine carrée de 3, la hauteur du triangle équilatéral. On peut aussi calculer la place occupée par chaque personne. Pour rappel, avec les points bleus, 9 personnes occupent un carré de 4 m de côté, dont l’aire est 16 m2. Cela fait un peu moins de 1,8 m2 par personne. Avec les points rouges, 7 personnes occupent un hexagone régulier de 2 m de côté. Sachant que l’aire d’une telle figure est environ 10,4 m2 on obtient cette fois seulement 1,5 m2 par personne. En conclusion, les rouges auront moins d’espace personnel pour bouger les bras mais ils resteront à une distance de sécurité de 2 m. Cela confirme la supériorité de la configuration en triangles, un résultat qu’il ne faudra pas oublier lorsque nous devrons faire tenir un maximum d’élèves dans une salle de classe.
C’est tout pour cette fois. J’espère que ces réponses étaient satisfaisantes sans être trop techniques. Je tiens à remercier tous ceux d’entre vous qui avaient une question et je m’excuse pour celles que je n’ai pas pu traiter.
Featured image credit: Shutterstock
About the Author :
Originaire de Bretagne, David Soquet a obtenu une maîtrise de mathématiques à l’Université de Rennes et est devenu enseignant au tournant du millénaire. Après avoir affuté ses compétences au collège de Chantilly, près de Paris, il a été recruté par le Lycée en 2008. Père de deux enfants, David est aussi passionné d’histoire des sciences et essaie de contrebalancer la rigueur essentielle à l’enseignement des mathématiques avec l’humour et une invitation aux découvertes. Sa propre curiosité l’a aussi amené à s’intéresser à des sujets aussi variés que l’origami modulaire, la mythologie nordique, le cinéma de Fritz Lang et la musique.