Alors c’est décidé, vous voulez changer la faïence de votre cuisine. Vous voyez ces petits carrés beiges tous les matins depuis des années et l’autre jour vous vous êtes dit que vous en aviez assez. Ce n’est pas la couleur qui vous gêne, mais la forme. Vous trouvez les carrés ennuyeux. Ce changement soudain est sans aucun doute lié à une récente visite au Metropolitan Museum. A la vue des magnifiques mosaïques de la section des arts de l’Islam vous avez eu l’idée d’essayer quelque chose de moins traditionnel.
Bien sûr, les carrés sont bien pratiques : faciles à couper, faciles à empiler et très facile à disposer sur une surface. La raison est simple, leurs côtés sont de la même longueur et leurs angles sont de la même mesure. Les figures qui partagent cette propriété sont appelées polygones réguliers et les carrées ne sont pas les seules. Les triangles équilatéraux – avec trois angles de 60° – sont aussi réguliers, mais les rectangles ne le sont pas car leurs côtés ne sont pas nécessairement tous de la même longueur. Comme nous allons le voir, il est possible de dessiner un polygone régulier avec un nombre quelconque de côtés du moment que les deux conditions sont respectées.
Il y au moins deux raisons qui justifient l’utilisation de polygones réguliers. Tout d’abord, cela permet de facilement obtenir un motif symétrique, un élément important de ce que les gens considèrent harmonieux. La symétrie et l’harmonie peuvent aussi être obtenues avec des polygones non-réguliers comme les rectangles ou aussi en combinant différentes figures ensemble – les fameuses tesselations – mais ici nous nous concentrerons uniquement sur les motifs les plus simples parce que c’est juste une cuisine, pas l’Alhambra. La deuxième raison pour laquelle les polygones réguliers sont une bonne idée est dû au fait que les « carreaux » doivent être assemblées sans laisser de trous. C’est pour cela que les cercles ne sont jamais utilisés. Ils laissent des trous entre eux et à moins de combler avec d’autres cercles plus petits, qui vont à leur tour créer des trous encore plus petits, ce n’est pas pratique. Cela rappelle la fameuse plaisanterie sur le fromage suisse : « Plus il y a de fromage, plus il y a de trous mais plus il y a de trous moins il y a de fromage. »
Quelles sont les possibilités, à part les triangles et les carrés ? Si vous avez visité le Met, vous savez que les hexagones sont très populaires. Les artistes musulmans ont utilisé ces polygones à 6 côtés un peu partout et il faut bien admettre que c’est une jolie figure, plus harmonieuse que le carré un peu terne ou le triangle équilatéral agressif. Les hexagones sont aussi familiers dans la nature, des alvéoles des ruches aux colonnes de basalte des Iles Britanniques[i]. Je suis sûr que vous vous souvenez de la première fois où vous avez eu le droit d’utiliser un compas. Vous avez tracé quelques cercles et ensuite votre maîtresse vous a montré comment dessiner une belle rosace en reportant le rayon autour du cercle pour obtenir 6 points.
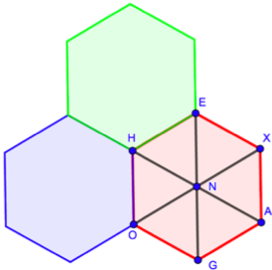Pourquoi les hexagones fonctionnent-ils ? C’est assez simple en fait, c’est juste une histoire d’angles. Si vous tracez les trois longues diagonales d’un hexagone, c’est assez facile de voir que vous pouvez le partager en 6 petits triangles équilatéraux qui font apparaître des angles de 60° dans tous les coins. Cette image vous rappelle peut-être à des souvenirs du jeu Trivial Pursuit ou à un morceau de camembert[ii]. Les 6 angles autour du point N mesurent 60° et leur somme est donc 360°, sans surprise puisque, comme le savez bien, un tour complet correspond à 360°. Nous pouvons aussi voir que les 6 angles extérieurs de l’hexagone – par exemple l’angle en H formé par les côtés HE et HO – mesurent 120°. Par suite, puisque 3 fois 120 font 360 vous pouvez comprendre pourquoi 3 hexagones s’emboîtent parfaitement et c’est ainsi que l’on peut recouvrir une surface entière.
Pour la même raison, nous pouvons paver le plan à l’aide de 4 carrés (4 fois 90°) ou de 6 triangles équilatéraux (6 fois 60°). Pour l’instant, nous avons trouvé 3 polygones réguliers pouvant servir de carrelage mais nous en avons oublié au passage. Qu’en est-il du polygone à 5 côtés, le fameux et mystérieux pentagone ? C’est mon préféré et il est un peu plus difficile à étudier.
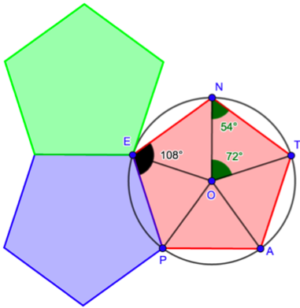Pour commencer, prenons un instant pour l’admirer dans toute sa splendeur, dessiné ici à l’intérieur de son cercle, quelque chose qui est toujours possible avec un polygone régulier. Je suis prêt à parier que celui-là vous ne l’avez pas dessiné en primaire[iii] mais comme pour l’hexagone on peut le découper.
Cette fois nous obtenons 5 triangles identiques et comme 360 divisé par 5 fait 72, les 5 angles autour du centre O mesurent 72°. Maintenant nous pouvons trouver les angles de chaque sommet (N par exemple) de la façon suivante :
Le triangle TON est isocèle parce que les deux côtés OT et ON sont des rayons du cercle. Par conséquent les angles en N et T ont la même mesure. Ensuite, je suis sûr que vous vous souvenez que la somme des trois angles d’un triangle est toujours 180° et comme O=72° nous savons qu’il reste 108° pour les deux autres. Mais nous avons dit qu’ils étaient identiques et donc chacun mesure 54°. Nous pouvons reproduire le même raisonnement dans chacun de s5 triangles et cela devrait suffire pour vous convaincre que les angles des sommets du pentagone, par exemple l’angle en E, mesurent 108°.
Et voilà d’où vient le problème ! Si vous placez trois pentagones côte à côte (comme sur le dessin), vous obtenez un trou de 36° parce que 3´108=324 qui est plus petit que 360°. Cela explique pourquoi vous ne pouvez pas recouvrir le mur de votre cuisine en utilisant uniquement des carreaux de forme pentagonale mais cela ne signifie pas pour autant que le pentagone n’est pas une figure intéressante[iv]. Par exemple, les fans et joueurs de foot savent très bien que les pentagones sont utilisés, avec des hexagones, pour former le ballon qui n’est pas une sphère parfaite mais en fait un icosaèdre tronqué : un magnifique solide possédant 32 faces dont 12 pentagones et le reste des hexagones. Cela peut sans doute vous amener à poser aux moins deux questions :
Comment ça un ballon de foot n’est pas rond ?- Icosaèdre tronqué ? C’est quoi ce truc ?
Commençons par la première question, de loin la plus simple. Contrairement aux ballons de basket synthétiques qui sont moulés pour former des sphères parfaites, la plupart des ballons de foot sont cousus en assemblant des pièces de cuirs plates. Le problème avec cette technique c’est qu’il est mathématiquement impossible de transformer une surface plane en sphère. Redisons ça une deuxième fois : il est impossible de prendre une feuille de papier et de la plier pour former une sphère comme on peut le faire, par exemple, pour un cube. Et cela n’est pas seulement dû au fait qu’il y a des parties « arrondies ». Après tout, il est possible de construire un cylindre en enroulant une feuille de papier rectangulaire de la même façon que certains improvisent parfois une longue vue à l’aide d’un magazine. Il est même possible de faire un cône en fait, il suffit d’enrouler sur elle-même une feuille de papier circulaire. Mais une sphère ? Il n’y a vraiment aucun moyen. Avez-vous déjà essayé d’emballer un ballon dans du papier cadeau ? Cela ne peut se faire parfaitement, il y a aura forcément du chevauchement. Cette difficulté topologique[v] est aussi la raison pour laquelle un planisphère ne peut jamais représenter correctement le globe. Vous avez certainement entendu parler de la projection de Mercantor, l’une des plus célèbres représentations de la planète qui porte le nom du géographe hollandais du 16e siècle et qui laisse à penser que le Groenland a la même superficie que l’Afrique alors que cette dernière est presque 15 fois plus grande.
Passons à la deuxième question. Comme vous le savez peut-être, un polyèdre est un solide ayant plusieurs faces en forme de polygones. Les plus connus sont le cube, le prisme – pensez Toblerone – ou encore les diverses pyramides. L’étude des polyèdres remonte à très longtemps et, comme pour les polygones, on s’intéresse aussi aux polyèdres réguliers dont toutes les faces sont identiques. Le cube, avec ses 6 faces carrées, est sûrement le plus connu de tous. Les pyramides égyptiennes, en revanche, ne sont pas régulières car elles ont 1 face carrée (la base) et 4 faces triangulaires. Une pyramide régulière a seulement 4 faces triangulaires, c’est un tétraèdre. Ce qui est surprenant avec les polyèdres réguliers, contrairement aux polygones réguliers, c’est qu’il n’y en a pas un nombre illimité. Il y en a en fait seulement 5 et on les appelle polyèdres de Platon, du nom du philosophe grec qui les a utilisés dans ses écrits. Voilà les membres de ce club très spécial : le tétraèdre (4 triangles) et le cube (6 carrés) déjà mentionnés, l’octaèdre (8 triangles) qui est en fait 2 pyramides égyptiennes collées par la base, le magnifique dodécaèdre avec ses 12 pentagones et enfin l’icosaèdre et ses 20 triangles.
Les amateurs de jeux de rôle connaissent bien ces solides car ils sont utilisés comme dés non cubiques. Ils se disent d’ailleurs peut-être que j’ai oublié le dé à 10 faces mais en fait celui-ci n’est pas un polyèdre régulier car ces faces ne sont pas des polygones réguliers.
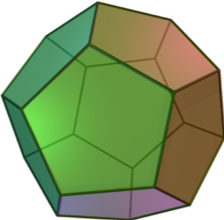Si vous jetez un œil au dodécaèdre, vous aurez peut-être un peu de mal à compter ses sommets et ses arêtes. Voilà comment procéder. Nous savons qu’il y a 12 pentagones et que chacun a 5 sommets. Cela peut nous faire croire qu’il y a 60 sommets en tout mais en fait nous avons compté chaque sommet plus d’une fois, 3 fois pour être exact car chaque sommet est connecté à 3 faces. En divisant par 3 on trouve 20 sommets. En utilisant la même logique, on voit que chaque sommet est connecté à 3 arêtes, ce qui donne 60 arêtes. Cette fois-ci, chaque arête relie 2 sommets et il faut donc diviser par 2, donnant ainsi 30 arêtes. Et voilà le dodécaèdre : 12 faces, 20 sommets et 30 arêtes.
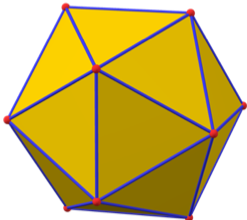C’est le moment idéal pour évoquer un merveilleux résultat découvert au milieu du 18e siècle par le grand mathématicien suisse Leonhard Euler. Pour chaque polyèdre – régulier ou non – la fomule Faces + Sommets – Arêtes = 2 est toujours vérifiée. Pour le dodécaèdre, vous pouvez vérifier que 12+20–30=2. Le cube donne 6+8–12=2, la pyramide égyptienne 5+5–8=2 et la boîte de Toblerone 5+6–9=2. C’est presque magique et cela peut être très utile quand les nombres deviennent plus grands et difficiles à déterminer. Pour finir, revenons à l’icosaèdre. Par définition, il possède 20 faces et avec la même méthode que pour le dodécaèdre, on trouve qu’il y a aussi 12 sommets et 30 arêtes. Sans surprise, on a encore 20+12–30=2.
Parfait, vous êtes prêts pour revenir au ballon de foot et finalement comprendre ce qu’est un icosaèdre tronqué. Comme son nom l’indique, vous pouvez partir du solide à 20 faces. Comme vous pouvez le voir, chaque sommet est relié à 5 arêtes dont les extrémités forment un pentagone. Maintenant, il vous suffit de suivre les instructions suivantes :
Étape 1: En partant d’un sommet quelconque, glissez jusqu’au tiers de chacune des 5 arêtes. Vous obtenez 5 points qui forment un nouveau pentagone plus petit.
Étape 2: Imaginez de passer un couteau le long de ce petit pentagone et de retirer cette petite pyramide. Cela donne une première face pentagonale. Sans être trop technique, les matheux appellent cela la section du solide par le plan contenant le pentagone.
Étape 3: Répétez les étapes 1 et 2 pour les 11 autres sommets. Vous avez maintenant 12 pentagones.
Étape 4: C’est la plus difficile – surtout si vous êtes aussi mauvais que moi pour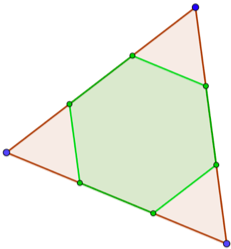
visualiser les objets en 3 dimensions – et pourtant il n’y a rien d’autre à faire que de prendre un peu de recul. Quand vous avez sectionné les sommets, avez-vous réfléchi à ce que sont devenues les 20 faces triangulaires ? Alors pour commencer les trois côtés de chaque triangle ont été réduits des deux tiers et on a gardé la partie centrale. Ensuite, les 5 points de l’étape 1 ont été reliés par la section, donnant 3 nouvelles arêtes. Au final, vous devriez voir que l’on obtient un hexagone. Personnellement, je le vois parce que ce n’est pas ma première fois mais si vous n’y arrivez pas, cette autre image devrait vous aider. L’hexagone vert est la nouvelle face et il y en a 20 en tout. Ça y est : 12 pentagones et 20 hexagones, c’est ça l’icosaèdre tronqué.
Et maintenant vous vous dites : « D’accord il y a 32 faces mais combien de sommets et d’arêtes ? » Pour les sommets c’est facile puisqu’on a remplacé chacun des 12 sommets de l’icosaèdre par 5 nouveaux. Ça fait 60. Ensuite, on peut utiliser la formule d’Euler pour trouver le nombre d’arêtes. Puisque 60+32=92 on sait qu’il doit y avoir 90 arêtes. C’est beaucoup mais c’est assez logique puisqu’il y a 12 fois 5 arêtes sur les pentagones et 20 fois 6 pour les hexagones, soit un total de 180 qu’il faut diviser par 2 puisque chaque arête connecte 2 faces.
Parfait ! Il est temps de dégager le ballon et de retourner dans la cuisine qui, comme je le répète à mon fils, n’est jamais un bon endroit pour jouer au foot. Maintenant que nous en avons fini avec le pentagone, nous pouvons nous intéresser au suivant : l’octogone[vi].
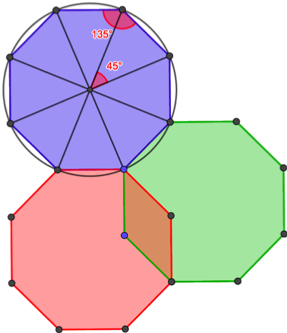
Avec la méthode utilisée plus tôt, on peut facilement déterminer que les angles intérieurs mesurent 45° (360 divisé par 8) et que les angles extérieurs mesurent 135°. Par conséquent, si on juxtapose deux spécimens on obtient 270° et il manque seulement 90° pour faire le tour complet. Si on ajoute un troisième octogone alors ça dépasse comme le montre l’image.
La méthode fonctionne toujours et on peut l’utiliser rapidement pour les polygones suivants (jusqu’au dodécagone à 12 côtés, en oubliant au passage le polygone à 11 côtés), surtout si on remarque que la somme d’un angle intérieur et d’un angle extérieur est toujours 180°.
- Le nonagone : angles intérieurs 40°, angles extérieurs140°.
- Le décagon : angles intérieurs 36°, angles extérieurs144°.
- Le dodécagone : angles intérieurs 30°, angles extérieurs150°.
Vous pouvez facilement le vérifier, aucun d’entre eux n’est utilisable pour du carrelage et on peut commencer à se demander si un autre polygone régulier pourrait fonctionner. Jusqu’à présent, seuls le triangle (angle extérieur de 60°), le carré (angle extérieur de 90°) et l’hexagone (angle extérieur de 120°) peuvent paver une surface et ça marche parce que les nombres 60, 90 et 120 sont des diviseurs de 360, une autre façon de dire que si on divise 360 par ces nombres le résultat est un nombre entier. Le diviseur suivant de 360 est 180 mais il est impossible que l’angle extérieur d’un polygone mesure 180° car c’est la mesure d’un angle plat et aucun polygone ne peut avoir un angle plat, encore moins tous ces angles plats. Pour voir ce résultat sous un autre angle (ha ha), essayons de généraliser en considérant un polygone régulier à n côtés, n étant un entier supérieur à 2 (parce qu’il faut au moins 3 côtés pour faire un polygone). Nous savons que ces angles intérieurs mesurent 360/n et donc que ces angles extérieurs sont 180–360/n qui peut aussi s’écrire (180n-360)/n. Pour savoir si ce nombre est un diviseur de 360 nous devons calculer le quotient 360/((180n-360)/n) qui, après quelques manipulations fractionnaires de niveau quatrième[vii], peut s’écrire 360n/(180n-360) et se simplifier en 2n/(n-2).
Voilà. Si vous avez survécu à tous ces calculs, vous savez que le résultat final 2n/(n-2) représente, si c’est un entier, le nombre de polygones à n côtés nécessaire pour couvrir un tour complet de 360° sans chevauchement. Essayons cette formule avec quelques valeurs de n :
- n=3 donne 2´3/(3-2)=6, six triangles équilatéraux.
- n=4 donne 2´4/(4-2)=4, quatre carrés.
- n=5 donne 2´5/(5-2)=10/3 qui n’est pas un entier.
- n=6 donne 2´6/(6-2)=3, trois hexagones.
- n=7 donne 2´7/(7-2)=2,8 qui n’est pas un entier.
- n=8 donne 2´8/(8-2)=16/6 qui n’est pas un entier.
- Etc…
Pour prouver une fois pour toutes qu’aucune autre valeur de n ne convient, réécrivons le nombre 2n/(n-2) sous la forme 2+4/(n-2) –je vous laisse une minute pour vérifier que c’est correct– pour voir que le seul moyen pour que ce nombre soit entier est que la partie 4/(n-2) soit elle-même un nombre entier et cela est possible si et seulement si n-2 est un diviseur de 4. Mais 4 possède seulement 3 diviseurs, à savoir 1, 2 et 4 et cela nous redonne les 3 valeurs de n déjà trouvées. Quod Erat Demonstratum comme disaient les Grecs. Nous sommes arrivés au bout. C’est peut-être une déception mais si vous ne voulez pas utiliser le carré ennuyeux ou le triangle trop simple, il apparaît que la seule possibilité raisonnable soit l’hexagone. A moins que vous ne souhaitiez vous inspirer d’Escher mais ça c’est une autre histoire…
———
[i] La Chaussée des Géants en Irlande du Nord en est un bon exemple.
[ii] C’est promis : plus de référence fromagère.
[iii] Sa construction au compas est possible mais bien plus difficile que celle de l’hexagone. Pour une solution plus rapide on peut utiliser un rapporteur.
[iv] Le Pentagone américain est un bon exemple, avec ses 5 côtés d’environ 281 mètres.
[v] La topologie est une branche fascinante des mathématiques qui se focalise sur la forme des objets, indépendamment de leur taille.
[vi] Je sais je sais j’en ai encore évité un mais faites moi confiance sur ce coup, vous ne voulez pas vous amuser avec le polygone à 7 côtés.
[vii] Pour diviser par une fraction, on peut multiplier par son inverse.
About the Author :
Originaire de Bretagne, David Soquet a obtenu une maîtrise de mathématiques à l’Université de Rennes et est devenu enseignant au tournant du millénaire. Après avoir affuté ses compétences au collège de Chantilly, près de Paris, il a été recruté par le Lycée en 2008. Père de deux enfants, David est aussi passionné d’histoire des sciences et essaie de contrebalancer la rigueur essentielle à l’enseignement des mathématiques avec l’humour et une invitation aux découvertes. Sa propre curiosité l’a aussi amené à s’intéresser à des sujets aussi variés que l’origami modulaire, la mythologie nordique, le cinéma de Fritz Lang et la musique.