So, you want to change the ceramic tiles in your kitchen. They’ve been in front of you for years and the other day you just decided you had enough of these small beige squares. The problem is not the color, what bothers you now is the shape. You find squares boring. This sudden change is obviously the result of a recent visit to the Metropolitan Museum. After admiring the beautiful mosaics in the Islam Arts section you’ve been thinking you could change the design of your own kitchen tiles, trying something less conventional.
Of course, square tiles are convenient: easy to cut, easy to stack and very easy to arrange on a surface. The reason for this is that their sides are of equal length and their angles are of equal measure. Shapes that share these properties are called regular polygons and squares are not the only ones. Equilateral triangles – with three 60° angles – are also regular, but rectangles are not because their sides are not necessarily the same. As we will see, you can basically draw a regular polygon with as many sides as you wish as long as you follow the two conditions.
There are at least two reasons for using regular polygons. The first one is that it makes it easy to keep the whole design symmetrical, an important component of what people consider harmonious. Symmetry and harmony can also be achieved with non-regular polygons such as rectangles or by combining different shapes together –the so-called tessellations– but here we will focus only on the simplest designs because it’s just a kitchen not The Alhambra. The second reason why regular polygons are a good option is that tiles need to be assembled together without leaving holes. That is why circular tiles are never used because they leave big holes between them and unless you’re willing to fill those with smaller circles, which will create additional smaller holes, this is not practical. This would almost look like the famous swiss cheese joke: “The more cheese you have, the more holes you get but the more holes you get the less cheese you have.”
What are your options, besides triangles and squares? If you’ve been to the Met, you know that hexagons are very popular. Islamic artists have used the 6-sided polygon everywhere and you have to admit it is a nice shape, certainly better looking that the dull square or the aggressive equilateral triangle. Hexagons are also popular shapes in nature, from the beehives’ cells to the basalt columns in the British Isles[i]. I’m sure you remember when, as a kid, you were allowed to use the compass for the first time. You traced a couple of circles and then your teacher showed you how to draw a nice rosette[ii] by duplicating the radius around the circle to get 6 points.
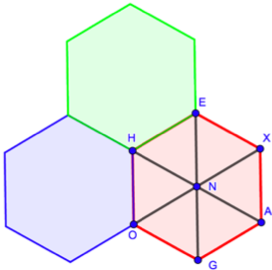Why do hexagonal tiles work? It’s quite simple actually, it’s only a matter of angles. If you draw the three long diagonals of a hexagon, it is easy to see that you can divide it in 6 small equilateral triangles which bring 60° angles everywhere. This image may bring back souvenirs of the board game Trivial Pursuit or a piece of camembert[iii]. The 6 angles around point N measure 60° and add up to 360°. No surprise there because, as you know, 360° corresponds to a full turn. We can also figure out that the 6 angles of the hexagon –for example the angle in H between sides HE and HO– measure 120°. Now, because 3 times 120 is 360 you should be able to see that 3 hexagons fit perfectly and that is how you can fill up the whole plane.
For the same reason, we can pave the plane by using 4 squares (4 times 90°) or 6 equilateral triangles (6 times 60°). So far, we have 3 regular polygons which can be used but we skipped one on the way. What about the 5-sided polygon, the notorious and mysterious pentagon? This one is my favorite, but a bit trickier.
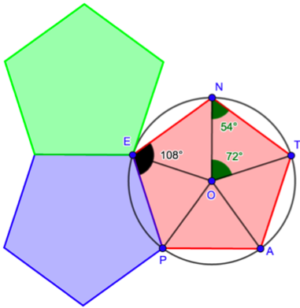First, let’s look at it in all its splendor, drawn here inside its circle, something that is always possible with a regular polygon. I bet you didn’t draw that one in 5th grade[iv] but just as we did for the hexagon we can divide it. This time we get 5 identical triangles and because 360 divided by 5 is 72, the five angles around the center O measure 72°. Now, we can figure out the angles at each vertex (for example N) in the following way:
Triangle TON is isosceles because segments lines OT and ON are both radii of the circle. This means that angles N and T have the same measure. Then, I’m sure you remember that the 3 angles of any triangle always add up to 180° and since we already have O=72° we know that the sum of the other 2 is 108°. But we said they were identical and that means each of them measures 54°. We can reproduce the same reasoning in each of the 5 triangles and that should be enough to convince you that the angles at the vertices, for example the angle at E, measure 108°.
And that’s where the cookie crumbles! If you put three pentagons next to each other (as in the drawing) you get a hole of 36° because 3 times 108 is 324 and this falls short of 360°. That explains why you can’t cover your kitchen wall using only pentagonal tiles but this doesn’t mean the pentagon is not interesting[v]. For example, fans and players know very well that pentagons are used, in combination with hexagons, to make a soccer ball, a ball which is not a perfect sphere but a truncated icosahedron: a beautiful solid with 32 faces, 12 of them pentagons and the rest hexagons. This may lead you to ask at least two questions:
What do you mean a soccer ball is not round?- What kind of weird animal is a truncated icosahedron?
Let’s start with the first question, the easy one. Contrary to basketballs which are molded into perfect spheres, most soccer balls are sewn by putting together flat pieces of leather. The problem with that technique is that it is mathematically impossible to turn a flat surface into a sphere. Let’s say that one more time: you cannot take a piece of paper and fold it into a sphere the way you would do it for a cube. And it’s not only because it has some “round” parts. After all, it is possible to build a cylinder by rolling a rectangular piece of paper the same way people sometimes use a magazine to improvise a spyglass. You can even make a cone for that matter, you just need to roll a circular piece of paper on itself. The sphere? There is just no way do it. Have you ever tried to wrap a soccer ball for a gift? Can’t be done perfectly. The paper will always overlap somewhere. This topological[vi] conundrum also explains why a planisphere can never precisely represent the globe. You may have heard of the Mercator projection, one of the most common representation of Earth in the northern hemisphere which is named after the 16th century Dutch geographer and shows Greenland as big as Africa despite the fact that the latter is almost 15 times larger.
Now, let’s tackle the second question. As you may know, a polyhedron is a solid with a certain number of faces which are in the shape of polygons. Common examples are the cube, the prism – think Toblerone chocolate bar– and various types of pyramids. Polyhedra have been studied for a long time and, just like polygons, we also consider the regular ones when all their faces are the same. The cube, with its 6 squared faces is arguably the most famous regular polyhedron. The classic Egyptian pyramids, however, are not regular because they have 1 squared face and 4 triangular ones. A regular pyramid would only have 4 triangular faces, what is called a tetrahedron. The surprising thing about regular polyhedra is that, contrary to regular polygons, there is not an unlimited number of them. There are actually only 5 and they are known as the platonic solids, from the Greek philosopher who wrote a lot about them. Here are the members of this very select group: the already mentioned tetrahedron (4 triangles) and cube (6 squares), the octahedron (8 triangles) which is simply made of 2 Egyptian pyramids stuck by their bases, the marvelous dodecahedron with its 12 pentagons and finally the icosahedron and its 20 triangles.
Roleplaying gamers are already familiar with these solids as they are classically used as non-cubic dices. They may actually think I forgot one because a traditional set also includes 10-sided dices. However, this one is not a regular polyhedron because its faces are not regular polygons.
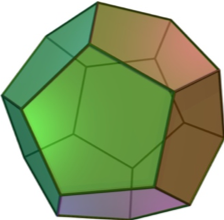If you take a look at the dodecahedron, you may find it difficult to count how many edges and vertices it has. Here is one way to do it. We know there are 12 pentagons and that each one has 5 vertices. That would lead us to believe that there are 60 vertices but this is forgetting that we counted them more than one time and more precisely 3 times since each vertex is connected to 3 pentagons. In the end we get 20 vertices. Using the same logic, we see that each vertex is connected to 3 edges, giving us 60 edges. This time however, each edge is connected to 2 vertices and we need to divide by 2, hence resulting in 30 edges. Here is the dodecahedron in a nutshell: 12 faces, 20 vertices and 30 edges.
Now seems the perfect time to introduce a wonderful result discovered in the middle of the 18th century by the great Swiss mathematician Leonhard Euler. For any polyhedron – regular or not – the formula Faces + Vertices – Edges = 2 is always verified. For the dodecahedron you can check that 12+20–30=2. The cube gives 6+8–12=2, the Egyptian pyramid 5+5–8=2 and the Toblerone’s box 5+6–9=2. This seems almost magic and can be very helpful when the numbers get bigger and hard to find. As a last example, let’s go back to the icosahedron. By definition it has 20 faces and with the same method we used for the dodecahedron we can figure out that it also has 12 vertices and 30 edges. Without any surprise we again get 20+12–30=2.
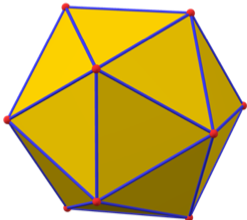Okay, you’re ready to go back to the soccer ball and understand what a truncated icosahedron is. As its name indicates, you can start with the 20 sided solid. As you can see in the image, each vertex is connected to 5 edges whose endpoints make a pentagon. Now follow these instructions carefully:
Step 1: Starting from any vertex, move alongside the 5 edges and stop at a third of the distance from the start, you will get 5 other points which will form another smaller pentagon.
Step 2: Imagine passing a knife along this pentagon and removing that tiny pyramid. You get your first pentagonal face. Without being too technical math people call this the section of the solid by the plane containing the pentagon.
Step 3: Repeat steps 1 and 2 for each of the 11 remaining vertices. Now you have 12 pentagons.
Step 4: That’s the tough one –especially if you’re as bad with 3D vision as I am– and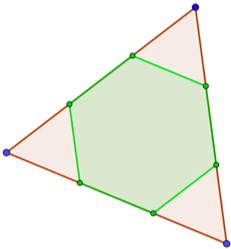
yet there’s nothing left to do except look back. When you sliced off the vertices, what do you think happened to the 20 triangular faces? Well first the three edges of each triangle were reduced by 2 thirds and we kept the middle part. Then all the 5 points from Step 1 were connected by the section, producing 3 new edges. In the end you shall be able to see that you get a hexagon. Personally, I do see it because I’ve had a lot of practice but if you can’t, this other drawing may help visualize what happened. The green hexagon is the new face and we get 20 of them. Here we are: 12 pentagons and 20 hexagons, that’s what a truncated icosahedron is.
Now you’re thinking: “Okay there are 32 faces on that thing but how many edges and vertices?” For the vertices, it’s quite simple because we replaced each of the 12 vertices of the icosahedron by 5 new ones. That’s 60. Then we can use Euler’s magic to figure out the number of edges. Since 60+32=92 we know we have 90 edges. That’s a lot but it actually makes sense because we have 12 times 5 edges for the pentagons and 20 times 6 for the hexagons, a total of 180 which we must divide by 2 because each edge is connected to 2 faces.
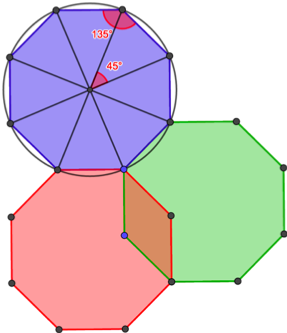Great! It’s time to kick the ball out and go back in the kitchen which, as I keep telling my son, is never a good place to play soccer. Now that we’ve dealt with pentagons, let’s consider the next one: the octagon[vii]. With the same method we already used before we can easily figure out that the interior angles measure 45° (360 divided by 8) and the exterior ones 135°. As a result, if we put 2 specimens next to each other we have 270° and we’re missing only 90° for a full turn. If we add a third octagon, there is overlap as you can see in the image.
The method always works and we can cover the next polygons (skipping the 11-sided one and ending with the 12-sided dodecagon) in quick fashion, especially if we notice that the sum of an exterior angle and an interior one is always 180°.
- The nonagon: interior angles 40°, exterior angles 140°.
- The decagon: interior angles 36°, exterior angles 144°.
- The dodecagon: interior angles 30°, exterior angles 150°.
As you can easily check, none of them are good for tiling and we may start to wonder if another regular polygon could work. So far, only the triangle (exterior angle 60°), the square (exterior angle 90°) and the hexagon (exterior angle 120°) could cover the whole plane and they do because 60, 90 and 120 are all factors of 360, another way of saying that if we divide 360 by these numbers the result is a whole number. The next factor of 360 is 180 but it is impossible for the exterior angle of a regular polygon to measure 180° because that’s the measure of a flat angle and no polygon can have one flat angle, let alone all of them. To see that result in another way, let’s try and generalize by considering the regular n-gon, a polygon with n sides, n being any integer greater than 2 (because you need at least 3 sides to make a polygon). We know that its interior angles measure 360/n and therefore each exterior angle is 180-360/n which we can also write (180n-360)/n. To see if that number is a factor of 360 we need to divide 360 by it and check if the result is an integer. That quotient is 360/((180n-360)/n) or, using some 8th grade fraction manipulations[viii], 360n/(180n-360) which can be simplified into 2n/(n-2).
There. If you’ve survived all these calculations, you know that this final result 2n/(n-2) represents, if it is an integer, the number of n-gons used to cover a full 360° without any overlap. Let’s try the formula for some values of n:
- n=3 gives 2´3/(3-2)=6, six equliateral triangles.
- n=4 gives 2´4/(4-2)=4, four squares.
- n=5 gives 2´5/(5-2)=10/3 which is not an integer.
- n=6 gives 2´6/(6-2)=3, three hexagons.
- n=7 gives 2´7/(7-2)=2.8 which is not an integer.
- n=8 gives 2´8/(8-2)=16/6 which is not an integer.
- Etc…
To prove once and for all that no other value of n will work we can rewrite the number 2n/(n-2) as 2+4/(n-2) –take a minute to double check that this is correct– and see that the only way this number can be an integer is if the part 4/(n-2) is itself an integer and that can happen if and only if n-2 is a factor of 4. But 4 has only 3 factors, namely 1, 2 and 4 and this gives us the only 3 values of n we already found. Quod Erat Demonstratum as the Ancient Greeks would say. We’ve reached the end. It may come as a disappointment but if you don’t want to use the boring square or the too simple triangle, it seems your only reasonable option is the hexagon. Unless you want to go full style Escher on that one…
———
[i] The Giant’s Causeway in Northern Ireland is a good example.
[ii] Which apparently is the English for « rosace ».
[iii] I promise: no more cheesy references after that point.
[iv] Its construction with a compass is possible but much more complicated than the hexagon. For a quick solution, yu can use a protractor.
[v] The US Pentagon is one good example with 5 sides of approximately 921 feet.
[vi] Topology is a fascinating branch of mathematics which focuses on the shape of objects, independantly of their size.
[vii] I know I know I skipped one again but trust me on this one, you don’t want to deal with the 7-sided heptagon.
[viii] To divide by a fraction, you can simply multiply by its reciprocal.
About the Author :
Originally from Brittany, David Soquet graduated from the Université de Rennes, before becoming a math teacher. After honing his skills at a middle school near Paris, he joined the Lycée Français in 2008. He is the father of two children and is passionate about the history of science. In his teaching, he tries to balance the rigor required by mathematics with humor and discovery. He is very curious and his interests range from modular origami and norse mythology to Fritz Lang’s cinema and music.