Chances are you never bothered to ask your math teacher where the words “sine” and “cosine” came from or why we use that ridiculous symbol for the square root of a number. You probably accepted these new notations – to be added to the already long list of arcane words and symbols mathematicians use – the same way you accepted in elementary school that a “vertical” cross is used for addition and the same cross slanted by 45 degrees is used for multiplication. Even if you were of the curious kind – the kind who asks his history-geography teacher why the Viking Erik the Red named “Greenland” the big chunk of ice he encountered after being exiled from Iceland[1] – you probably thought that knowing the symbol “=” first appeared in 1557 in a book published by the Welsh mathematician Robert Recorde was not fundamental to your understanding of algebra.
I get that, and I agree that ideas are more important than notations and symbols that are often the result of arbitrary decisions or historical incidents on par with the rule against split infinitives in English or the rule that says caillou should take an “x” in its plural form but not bisou. Math uses its own language and, like every language, it has evolved over time. Yes, the French mathematician Nicolas Oresme (1320;1382) would find it difficult to understand a modern book of algebra[2] but the same can be said of Chaucer and a modern translation of his famous tales. The only difference is that, out of laziness and willingness to be concise, mathematicians have a tendency to use shortcuts in lieu of long sentences. To give you just one example, try to figure out what the French philosopher Pierre de la Ramée meant when he wrote L27 ad L12 gives L75 in 1569[3].
However, when mathematical vocabulary is introduced – a necessity if one doesn’t want to follow the path of the English logicians Russell and Whitehead who tried to write all the math in symbolic notation in their early 20th-century book Principia Mathematica – one can see that etymology plays an important role if only to understand the differences between such basics words as “tri-angle”, “quadri-lateral”, “poly-gon” or “tetra-hedra”. The fact that the first two have Latin roots (from latus, side and angulum, angle) and the last two Greek ones (from gonia, corner and hedra, face) illustrates the richness of our language but can also make us wonder about the sad fate of exotic shapes named tetralateral, trigon, or quadrangle. Well, if you’re thinking “Oh come on, tetralateral doesn’t make sense because it mixes a Greek prefix with a Latin suffix!” you are absolutely right but it turns out quadrangle is actually used by mathematicians (and is different than a quadrilateral) and trigon of course shows up in the word trigonometry.
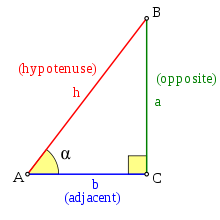I have always enjoyed etymology. I don’t know if it comes from my studying German and Latin in middle school or, for that matter, from my appreciation of puns and limericks, but I have always been fascinated by the construction, history and evolution of words. When I started teaching I enjoyed the fact that octopus could help my 6th graders remember that an octagon has eight sides but I also knew I had to be prepared for the question: ”Sir, what about October, shouldn’t it be the eight month of the year?” I also personally believe that being in math class is no excuse for bad spelling. Take the word hypotenuse for example. Too many students spell it with an extra “h” after the “t” even after being told it is incorrect. They know that, unless hippopotamus and hippocampus, the longest side of a right-angled triangle has little to do with horses and can only wonder why English uses seahorse for the latter but not seariver for the former. Then, because of the Greek root hypo (which means under or inferior) students associate hypotenuse with the more familiar hypothesis. However, whereas thesis means proposition and explains that a hypothesis is a sort of inferior proposition because it is not sure, tenuse comes from the verb teino and means to stretch, to extend. In other words, because the main characteristic of a right-angled triangle is its 90° angle, the hypotenuse is defined as the side extended under that angle. Similarly, I think that knowing that the Greek root skelos means leg helps remember why isosceles – which characterizes a triangle with two equal (iso) sides – is spelled that way.
Don’t get me wrong, I dig numbers, I always have. I have very early memories of manipulating them with ease and it is difficult for me to see a number somewhere – be it a birth date or a license plate – without adding or multiplying its digits to see if something will come out of it. As an example, when my brother turned 40 in 2014 I was very happy to tell him that the prime factorization[4] of 2014 is 2×19×53 and that the sum of the three numbers, 2, 19 and 53 is 74 which, of course, is the year of his birth. Results like that cannot be discovered if you’re not looking for them and playing with numbers requires good abilities in mental calculations as well as practice. If it is true that I have reached a certain proficiency in that domain – what else would you expect from a math teacher? – I am far from reaching the level attained by the great Indian mathematician Srivanasa Ramanujan or, for that matter, by our famous and relentless Mr O, who keeps challenging his students with mental methods[5].
I had not initially planned to mention the Indian wunderkind but since you insist I will tell you more about him. Ramanujan was born in India in 1887 and quickly became a phenomenon among his classmates because he could recite dozens of decimals of pi. As impressive as this sounds, memorizing digits is not such an incredible mathematical feat and Ramanujan would not be remembered today if he had done only that. The truth is that he had actually found formulas on his own to calculate these decimals and these formulas – as well as other works – were so incredible and unusual that they were rejected as incomprehensible by English mathematicians to whom Ramanujan’s impressed and overwhelmed teachers had sent them. As the story goes, only one of them, H. G. Hardy, found interest in Ramanujan’s formulas and decided it was worth inviting him to Cambridge… Words! Words! I meant to speak about words, not numbers. If you want to know more about Ramanujan and what’s so special about number 1729, check out his recent biopic “The Man who knew Infinity”.
As far as I’m concerned, I don’t see any difference between my ability to play with numbers and my ability to play with words. The reflexes are the same, switching letters or digits, showing the same appreciation for palindromes as words or numbers. However – and I’m sur Mr. O would agree with me – the reception by the audience is quite different. People who like to play with words are usually well accepted by society. They come in a long tradition of “l’esprit à la française”. They have wit, are called punsters and because of the possibility to play with sounds, they can even include poets. The universal respect given to crosswords’ creators and solvers is another illustration of this.
On the other hand, people who play with numbers are irrevocably seen as nerds and I believe one reason for this is that mathematics have an aura of complexity which they don’t necessarily deserve. As bad and widespread as illiteracy is in the world, it is possible that innumeracy is even worse but society doesn’t frown upon not knowing how much 7 times 8 is or how to take 20% of $60 as much as it does on bad spelling or bad writing[6]. Adults are never ashamed of admitting that they are bad at math – even worse, they are sometimes proud about it – but we don’t see many being boastful about their bad spelling or their not remembering the date of Pearl Harbor. This particularity of mathematics is also the reason why almost anyone can laugh at the famous History/Geography Bac’s bloopers (les perles du bac) such as « A megalopolis is the grouping of different cities in the shape of a banana. » or « After the war, Pétain was judged as the communist chief of the resistance »[7] whereas very few would understand why I laughed out loud when I encountered a lengthy and circular use of the parallelogram rule of vectors in a Terminale S paper a couple of years ago[8]. You might think it is not nice to poke fun at someone struggling in math but then why did you laugh at the banana thing ?
The same goes for jokes and when the great Edgar Alan Poe writes[9], talking about two of his fellow poets, that « To speak algebraically : – Mr. M. is execrable, but Mr. C. is x+1-ecrable. » it only reminds us that mathematical puns are the first sine of madness. And yet, I believe that anecdotes and etymology can help remember and understand the technical vocabulary used in math and maybe lift the veil of complexity that prevents people from focusing on ideas.
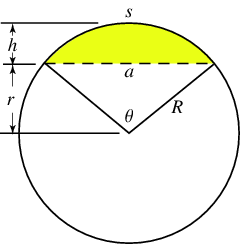Take the word chord for example. My New Oxford American Dictionary[10] tells me that its use in music originates from the Middle English cord, a shortening of the word accord. This makes sense since it is a set of harmonious notes. The « h » was added later on to avoid the confusion with cord which is another word for rope or string (think spinal cord). Now comes the tricky part. In math, a chord is a segment line joining two dots on a circle. It is so because a part of a circle is named an arc. We have the bow and the bowstring. But then shouldn’t it be cord ? Well it turns out the word comes from the Latin chorda. The French ditched the « h » for both meanings (the one for rope and the mathematical one) but, for some reason, the English kept it for the circle and, as a result, it may be difficult for an American to see the link[11].
Wait, it gets better. The Greek mathematician Hipparchus, arguably the father of trigonometry, was the first, in the 2nd century BCE, to compile tables linking the lengths of chords to the corresponding angles in a circle. A few centuries later, the Indian astronomer Aryabatha improved the method and naturally translated the word chord by jiva, Sanskrit for string. After going through the hands of Arab mathematicians (jiva became jiba), Aryabatha’s work arrived in Europe again and was translated into Latin in the 12th century. Because it was written without vowels, jiba was misinterpreted as jaib, the arab word for cavity or pocket. This brought the Latin sinus which, you guessed it, gave us sine and cosine. There you have it, in case you were wondering, there is absolutely no real connection between these two words and your nose. Knowing that the intended word was chord (or cord) and explaining the original method would help students remember that trigonometry deals with circles and angles.
Another of my favorite is the word digit. Unless they read a lot of biology or archeology magazines, Americans and English speaking people in general may have difficulties understanding its connection to anything else than numbers. Ever since computers and their strings of 0s and 1s have started dominating everything, people understand that they live in a digital world. They use digital cameras and read the digital version of their favorite newspaper online, whereas the French read la version numérique. Everything that is digital in English is numérique in French and there is an easy explanation for that. The word digit comes from the Latin digitus (finger or toe) something that is easily recognizable in « empreintes digitales », the French for fingerprints. Of course, it also gave us the word doigt and because we’ve always used our fingers[12] to count, this comes as no surprise that it took that meaning as early as the 14th century. But if that is so, where does the French equivalent chiffre comes from? That’s another interesting story. As you may know, the so called arabic numerals were actually invented by Indian mathematicians who developed a place-value system as early as the 1st century BCE. Instead of the 0 we now use they, at first, simply wrote a dot to designate an empty space. It was called śūnya the Sanskrit word for void or emptiness and, after the mathematician Brahmagupta defined it as a number for the first time in 628CE, it was translated into sifr by the Arabs. From there, two things happened. First, the word became zefiro in Latin, the root to the word zero in French as well as English[13]. More interestingly, sifr also changed into the Latin cifra which is the origin for chiffre. This means that the same Arab word brought to the French language the word for digit as well as the name of one particular digit, the zero. Do we find sifr in English? Yes! In the word cipher which is used in cryptography, the art of the secret code.
Math terminology and symbology are full of such stories which, I understand, may not be fascinating to anyone not directly concerned, but can at least explain why and how some words are used. I could tell you in details how the study of “La Disme” – a short text published in 1588 in which the Dutch mathematician Simon Stevin explains the decimal system – helped me explain to my bilingual 6ème students the link between the English dime and the French dîme as well as illustrate how the iconic “accent circonflexe” replaced the “s” present in the Latin roots of many words such as château/castle, forêt/forest, coût/cost, maître/master…etc. I could also explain how both words algebra and algorithm come from a masterpiece by a 9th-century Persian mathematician from Baghdad[14] but to conclude this story I’d like to speak about one last word, a word that, at first glance, seems out of place in mathematics. I’m talking about calculus which, in English, is the name given to the field of mathematics dealing with continuous change and jointly “discovered” by Leibniz and Newton in the 17th century. Just like the French calcul, the word originates from the Latin calculus which means “small pebble” (petit caillou). What is the link between math and small stones? It is well documented that, at the time of ancient Greeks and Romans, counting stones were used together with an abacus which, before becoming what is still used today in some Asiatic countries, was a simple counting board. In the same vein, the famous Pythagoras is often imagined representing numbers with small stones in the sand. This is the reason why, out of all the calculs they have encountered in their life, French math teachers only fear one, le calcul rénal…
———
[1] Although there may have been a few more trees before the arrival of the Vikings, historians believe Erik the Red named it so to lure settlers into believing this was a profitable land. [2] Mostly because of all the letters, an idea that would be introduced 200 years later by the French François Viète. [3] L was a shortcut for the Latin “Latus” which means side. L27 simply means “the side of a square whose area is 27” an early notation for the square root. [4] Every integer can be written as the product of primes numbers. Prime numbers are numbers who have only 2 divisors such as 2, 3, 5, 19 or 53. In case you’re wondering, the prime factorization of 2019 is 3×673. [5] I’m sure I don’t need to tell you the story of O. [6] Something John Allen Paulos explained in his 1988 book Innumeracy: Mathematical Illiteracy and its Consequences. [7] These are real mistakes from the 2018 exam, found here http://etudiant.aujourdhui.fr/etudiant/info/perles-du-bac-2018-le-best-of-de-l-epreuve-d-histoire-geographie.html [8] I kept a screenshot of it if you’re interested. [9] In his critique of James Russel Lowell. [10] Source of most of the following etymological information. [11] I guess the fact that a musician plays chords on a string instrument just adds to the joke. [12] Ironically the word “finger” comes from the Proto-Germanic “fingraz” which may be connected to an old word meaning “five”. That surely gives another look at the expression “give me five”. [13] The word “sifer” for 0 can also be found in old English books of arithmetics. [14] Muhammad ibn Musa al-Khwarizmi in the book “al-jabr wa’l-muqabala”.About the Author :
Originaire de Bretagne, David Soquet a obtenu une maîtrise de mathématiques à l’Université de Rennes et est devenu enseignant au tournant du millénaire. Après avoir affuté ses compétences au collège de Chantilly, près de Paris, il a été recruté par le Lycée en 2008. Père de deux enfants, David est aussi passionné d’histoire des sciences et essaie de contrebalancer la rigueur essentielle à l’enseignement des mathématiques avec l’humour et une invitation aux découvertes. Sa propre curiosité l’a aussi amené à s’intéresser à des sujets aussi variés que l’origami modulaire, la mythologie nordique, le cinéma de Fritz Lang et la musique.