Quand un professeur français arrive au LFNY, il y a quelques petits détails auxquels il doit s’adapter, et je ne parle pas du calendrier par cycle de 7 jours puisque cette nouveauté n’est pas réservée aux professeurs français, ni aux nouveaux d’ailleurs. Non, je pense plutôt à ces petits détails qui font partie de la vie à l’américaine – tel que le double symbolisme de la pomme pour un enseignant new yorkais – et je me propose d’en passer quelques-uns en revue ici.
Tout d’abord, il y a bien sûr l’échelle des températures en Fahrenheit et je dois dire qu’arriver à New York au milieu de l’été est le moyen parfait pour comprendre très vite ce que « plus de 90 degrés » signifie, même si cela n’atténuera pas l’effet de surprise quand les températures descendront à 0° Fahrenheit et que vous commencerez à bien ressentir les « Vents de l’hiver »[1]. Ensuite, une fois que vous êtes bien familiarisés avec cela[2], une autre chose importante à maîtriser est le système non métrique et là – je préfère vous prévenir – c’est beaucoup plus délicat, à tel point que vous trouverez peut-être plus simple d’essayer de convaincre les Américains de changer plutôt que d’apprendre leur système archaïque et mal fait. Et je pèse mes mots. C’est un exemple des quelques paradoxes de ce pays capable d’accomplissements incroyables (#RioOlympics) et en même temps toujours incapable d’instaurer l’équivalent du « Pass Navigo » dans le métro ou de mettre en place un système de vote simple et logique, comme vous vous en rendrez certainement compte dans un ou deux mois. Certes, vous serez un peu optimiste quand vous aurez effectué votre première conversion de pieds carrés en mètres carrés mais en vérité l’impression générale sera plutôt du type « Ah oui, il est petit mon studio dans l’UES. » Soyons francs, convertir n’est pas la solution. Pour ce type de problème, je recommande l’immersion totale.
Mais vous avez de la chance. Il s’avère que deux jours après la rentrée des classes commence la saison NFL et je crois personnellement qu’il n’y a pas de meilleur moyen pour découvrir les yards, feet et inches (pouces) que de regarder un match de football américain[3], le sport dont le ratio J’aime-regarder/J’aimerais-que-mes-enfants-y-jouent est sans doute le plus élevé parmi les sports majeurs. Même si vous ne comprenez pas toutes les règles tout de suite, cela vous permettra d’obtenir une compréhension globale des unités de mesure à l’échelle humaine et si vous voulez approfondir vous pouvez simplement retenir que 1 yard vaut 3 pieds et 1 pied vaut 12 pouces[4]. De plus, cela vous aidera à comprendre les conversations de certains de vos collègues ou élèves les lundis matins.
Une fois le mois d’octobre arrivé, quand débute la saison NBA, vous serez certainement assez à l’aise pour comprendre que si la plupart des basketteurs mesure entre 6 et 7 pieds, vous mesurez certainement entre 5 et 6. Et enfin, si vous êtes assez curieux et motivé pour regarder du baseball, le mois d’octobre est aussi la saison des playoffs et même si il y a peu de chances pour que vous puissiez voir un match des Yankees parce qu’ils ne seront sans doute pas qualifiés[5], voir une balle fuser à près de 100 mph vous donnera une petite idée de l’unité de vitesse utilisée ici, peut-être pas très précise mais certainement meilleure que celle de la limite de 25 mph évaluée en prenant un taxi jaune.
Si je m’amuse un peu avec tout ça c’est parce que ces petites difficultés seront sans doute peu problématiques en comparaison à une autre qui risque de vous embêter au quotidien : le format de papier. Comme vous l’avez sans doute déjà remarqué en utilisant la photocopieuse, le format de papier utilisé aux Etats-Unis est différent de celui utilisé en France. Pour être plus précis, parmi les presque 200 pays du monde, seulement 3 n’utilisent pas le format que les professeurs français connaissent : le Mexique, le Canada et les Etats-Unis[6]. Comme je l’expliquerai plus en détails plus tard, le format traditionnel A4 mesure 210 millimètres par 297 millimètres (ou 8.27 par 11.69 pouces) alors que le format américain le plus utilisé – appelé letter – a pour dimensions 8.5 par 11 pouces (ou 216 mm par 279 mm). Autrement dit, une page américaine est plus large de 6 mm mais plus courte de 18 mm. Ca ne parait pas beaucoup mais, comme nous le verrons, cette petite différence a des conséquences qui peuvent aller de 1 à 10 sur l’échelle de pénibilité et qui sont aussi intéressantes d’un point de vue mathématique.
Commençons par les petits problèmes. Premièrement, au cas où vous vous posiez la question, certains de vos élèves utiliseront des feuilles au format américain et d’autres au format français et quand vous les récupérerez après un test ou un quelconque travail écrit, elles seront mal alignées. Les sujets de test dépasseront des copies doubles françaises – un concept qui, à ma connaissance, n’existe pas aux Etats-Unis – et ces dernières seront plus hautes que le reste du paquet. Bien entendu vous pouvez décider d’imposer un format à votre classe mais vous risquez de vous apercevoir rapidement que les utilisateurs des fameux blocs notes de feuilles jaunes résistent au changement, surtout quand on peut acheter un lot de 12 blocs pour le même prix qu’un paquet de feuilles Clairefontaine. Vous vous y habituerez rapidement.
Parlons maintenant de vos documents. Si vous avez apporté plusieurs cours papier au format A4, vous ne pourrez pas les copier tels quels au lycée. Soyez prêt à les réduire (je suggère 93%) ou à perdre vos titres ! Et si vous pensez que tout va bien parce que tous vos documents sont en version digitale, vous risquez de déchanter car il y a de fortes chances qu’ils soient enregistrés au format A4 et que vous deviez les transformer au format américain. Cela semble simple a priori et ça l’est en effet si votre document contient essentiellement du texte et aucune référence aux numéros de page. Cependant, si vous avez des images, des graphiques ou encore plusieurs titres cela peut devenir très vite frustrant de tout arranger, surtout si vous aimez donner un document présentable aux élèves.
Parfait. Maintenant que j’ai évoqué les problèmes de réduction, je crois que c’est le moment idéal de poser cette question fondamentale : pourquoi le système utilisé en France (et presque partout ailleurs à l’exception de l’Amérique du Nord) est-il supérieur et comment a-t-il été obtenu ? Pour expliquer cela, il est nécessaire que je parle d’abord de pellicules d’appareil photo et d’échelle. Cela peut sembler surprenant à la plupart de nos élèves mais il fut un temps où un appareil photo et un téléphone étaient deux objets différents, une époque lointaine où il fallait mettre une pellicule dans un appareil photo avant de l’utiliser et apporter ensuite cette pellicule dans un magasin pour pouvoir voir le résultat. De façon un peu amusante, j’ai repensé à ces petits détails récemment lorsque ma fille est partie pour sa première longue sortie scolaire au printemps dernier et était autorisée à apporter un appareil photo jetable. Je pensais personnellement que ces choses n’existaient plus jusqu’à ce que nous en trouvions finalement un dans une pharmacie à côté de chez nous, à la plus grande joie de ma fille. Je lui ai expliqué comment l’utiliser et quand elle est revenue après 3 jours de découvertes éclaboussantes, elle a dit qu’elle avait prise 2 ou 3 photos mais qu’elle n’était pas sûre d’avoir bien « réarmé » l’appareil à chaque fois. Du coup, quelques semaines plus tard, j’ai décidé d’utiliser la vingtaine de poses restantes pour la graduation de grande section de mon fils et le pique-nique qui suivait. Et juste après avoir été pris en photo avec ses meilleurs copains, mon fils m’a demandé « Je peux voir ? », un réflexe qu’il a depuis tout petit lorsque j’utilise un appareil numérique.
Il s’avère que les photos étaient très mauvaises – surtout celles prises dans l’auditorium avec le flash de pacotille – mais au moins l’une d’entre elles pouvait justifier un encadrement pour un envoi à Grand-mère. Avant cela il serait nécessaire de l’agrandir et c’est là qu’intervient la notion mathématique d’échelle. Cela peut sembler évident à tout le monde mais quand vous voulez agrandir (ou réduire) une image, vous devez le faire dans les deux dimensions si vous voulez que votre image ait le même ratio. Sinon, le visage de votre enfant sera aplati comme dans un miroir déformant. Le ratio d’un rectangle est simplement le quotient de sa longueur par sa largeur et est parfois exprimé avec deux nombres comme dans le cas des écrans 4:3 et 16:9. Si vous doublez la longueur et la largeur d’une image, ce ratio ne change évidemment pas mais en revanche l’aire est 4 fois plus grande. Si vous ne le voyez pas, dessinez un rectangle, doublez les longueurs des côtés et vous pourrez voir que le nouveau rectangle peut contenir exactement 4 exemplaires de l’original. Ce résultat est valable pour toute figure bidimensionnelle, que ce soit un triangle, un polygone quelconque ou encore un cercle[7]. Si vous agrandissez ou réduisez toutes les longueurs d’un facteur k (c’est-à-dire que toutes les longueurs sont multipliées par k) alors l’aire sera multipliée par le carré de k (k2 ou k×k). C’est pour cette raison qu’il y a 100 millimètres carrés dans un centimètre carré. Ça n’est franchement pas très compliqué mais cela amène un petit problème très intéressant que je vous soumets ici :
Dessiner un carré et, sans calcul ni mesure, dessiner un 2e carré dont l’aire est exactement le double du premier carré.
Aussi simple que puisse paraître ce vieux problème, il est possible que vous ne trouviez pas la réponse tout de suite donc n’hésitez pas à arrêter de lire pour vous concentrer dessus ou bien à y réfléchir après avoir terminé la lecture. Je ne donnerai pas la réponse de toute façon.
Le problème avec le carré – avec tous les carrés – c’est que le ratio des côtés est évidemment 1 et quel que soit le facteur d’agrandissement ou de réduction il restera 1. Nous savons déjà que doubler les côtés du carré (un facteur d’agrandissement k=2) ne donne pas la bonne réponse car l’aire sera 4 fois plus grande. Peut-être une fois et demie plus grand ? Comme 1.5×1.5=2.25 c’est encore un peu trop grand. Je vous laisse vérifier que 1.4 est proche mais trop petit. Vous l’avez deviné, nous cherchons le nombre k tel que k2=2 et comme vous vous en souvenez sans doute, c’est exactement la définition de la racine carrée de 2 (notée Ö2) dont la valeur est environ 1.41421356237… Et non, cela ne donne pas vraiment la solution au problème car, souvenez-vous, vous ne pouvez faire ni calcul ni mesure et devez au contraire trouver une façon géométrique de doubler le carré. Cependant, la racine carrée de 2 est le lien mathématique avec notre problème de format de papier.
Revenons à notre feuille de papier rectangulaire et prenons 1 pour le petit côté et Ö2 pour le grand[8] ce qui donne bien sûr un ratio de Ö2. Plaçons maintenant deux exemplaires identiques de cette feuille côte à côte le long du grand côté pour obtenir un rectangle d’aire deux fois plus grande. Les dimensions du nouveau rectangle sont Ö2 et 2 et son ratio est aussi Ö2 car 2 divisé par Ö2 est Ö2. Autrement dit, le deuxième rectangle est un agrandissement à l’échelle du petit. Une autre façon de s’en assurer est de constater que la longueur et la largeur ont toutes les deux été multipliées par Ö2. C’est tout à fait logique puisque l’aire a été multipliée par 2. Pour finir, prenons encore un exemplaire de notre feuille de départ et coupons la en 2 par le grand côté. Nous obtenons un petit rectangle dont les dimensions sont 1 (la largeur intacte qui devient la longueur) et la moitié de Ö2 ou Ö2/2. Pour calculer le ratio de ce nouveau rectangle, il faut diviser 1 par Ö2/2. Je ne sais quels sont vos souvenirs sur la division par une fraction mais – faites-moi confiance – le résultat est encore Ö2 et cela signifie que le petit rectangle est une réduction – encore une fois, à l’échelle – du premier. Cette fois-ci, les dimensions ont été divisées par Ö2 (et l’aire par 2).
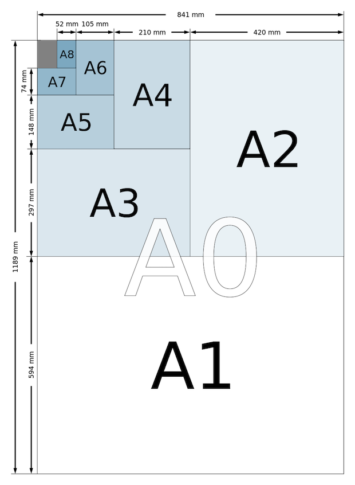
Cette propriété intéressante du nombre Ö2 – et vraie pour aucun autre nombre – fut remarquée par le scientifique allemand Georg Christoph Lichtenberg en 1783[9] et inspira très vite les révolutionnaires français qui, après avoir créé le mètre et ses dérivés (y compris le litre et le kilogramme) en 1793[10], promulguèrent la « Loi sur le timbre[11] » qui permettait de déterminer les taxes sur le papier selon les formats utilisés. On peut voir dans cette loi que le format appelé « Moyen papier » correspond exactement au format connu aujourd’hui sous le nom A3 dont les dimensions sont 420 et 297 millimètres. Si vous vous souvenez des nombres donnés plus haut, vous pouvez remarquer que ce format est obtenu avec deux feuilles A4 (297 par 210) et c’est exactement de cette façon que fonctionne le système, le standard international appelé ISO 216[12]. Avec deux feuilles A3 on obtient le format A2 (594 par 420) qui donne ensuite le A1 (841[13] par 594) et finalement le A0 (1189 by 841). Dans l’autre sens, si on coupe en 2 une feuille A4, on obtient le A5 (210 par 148) etc… jusqu’au très petit A10 qui mesure 37 par 26 mm.
Et voilà ! Si vous copiez 2 pages A4 dans une machine le résultat sortira sur une feuille A3. Et là, les Américains se disent « Heu…je ne sais pas si j’ai bien suivi mais si on met deux feuilles au format letter (11 pouces par 8.5 pouces) dans la photocopieuse on obtient une feuille de dimension 17 pouces par 11 pouces qui est exactement le format américain appelé ledger. Je ne vois pas ce que votre système a de spécial. » Et ils ont absolument raison ! C’est d’ailleurs pour cela que l’autre type de papier disponible au Lycée est de format 17 par 11. Sauf que… Sauf que j’ai une question : que se passe-t-il si j’ai seulement une page et que je souhaite l’agrandir au format suivant ?
Bon, il est possible que vous n’ayez pas bien compris le lien entre le ratio de Ö2 de Lichtenberg et le format de papier français parce que je ne vous ai pas demandé de faire les calculs. Faisons-les maintenant. Pour le A4 on a 297/210»1.414 et pour le A3 c’est 420/297»1.414. Je vous laisse faire les autres pour vérifier que tous les formats de la série A[14] ont un ratio égal à Ö2. Ce n’est pas très surprenant car, comme nous l’avons vu précédemment, si le premier a ce format alors tous les autres obtenus par doublement ou réduction de moitié ont forcément le même. C’est cette aspect qui est fondamental. Quand on agrandit ou réduit un document on ne change pas son ratio. Cela signifie que notre image au format A4, une fois agrandie, s’ajustera parfaitement sur une feuille A3. De même, si vous avez deux pages de votre cours au format A4 que vous souhaitez réduire à une seule feuille A4 avant de les photocopier pour vos élèves parce que votre école applique une politique « Go green », il vous suffit, en France, de poser les deux feuilles sur la machine et d’appuyer sur le bouton « A3 vers A4 ». Aucun contenu ne sera perdu et aucune bande blanche n’apparaîtra.
Ça ne fonctionnera pas au lycée. Pourquoi ? Simplement parce que le ratio des deux formats les plus utilisés n’est pas le même. Pour le format letter c’est 11/8.5»1.294 et pour ledger c’est 17/11»1.545. Et comme ils disent ici c’est là que « le gâteau part en miettes[15] ». Si vous voulez agrandir une feuille letter pour la mettre au format ledger, il n’y a pas de bouton automatique. Il faudra préciser de quel facteur vous voulez l’agrandir. Si vous utilisez un facteur de 1.3 (ou 130%) le résultat sera un document de 11.05 pouces sur 14.3 pouces et cela signifie qu’il y aura une bande blanche de presque 3 pouces de large sur la feuille. Dans l’autre sens, si vous essayez de réduire deux feuilles au format letter pour qu’elles passent sur une seule, il faudra réduire à 65% pour que la longueur de 17 pouces de l’original ne dépasse pas les 11 pouces de la copie. La conséquence de cette réduction sur la largeur est une bande blanche de 1.35 pouces. Par ailleurs, si vous voulez éviter la bande blanche et décidez de réduire votre document à 77% de sa taille d’origine, sa longueur sera supérieure à 13 pouces et vous perdrez 2 pouces de contenu. Il n’y a aucun moyen de contourner ce problème parce que, comme nous l’avons vu, un agrandissement ou une réduction à l’échelle doit se faire de façon uniforme si on veut éviter d’obtenir des photos déformées. Cela illustre l’incroyable supériorité du système ISO 216 et on peut se demander pourquoi les Américains refusent encore de l’adopter.
Trois questions demeurent.
#1 Comment les dimensions du format A0 ont-elles été choisies ? C’est en fait très simple. Les réformateurs français sont partis d’une grande feuille de 1 m2 (mètres carrés) et puisque la feuille devait avoir un ratio égal à Ö2, il s’agissait de trouver 2 nombres a (pour la longueur) et b (pour la largeur) vérifiant les égalités a×b=1 et a/b=Ö2. Un peu d’algèbre donne a=ÖÖ2 (la racine carrée de la racine carrée de 2) et b=1/a (l’inverse de a). Les valeurs approchées de ces nombres sont a»1.189207 m et b»0.84089 m et cela explique le choix de 1189 et 841 mm pour le format A0.
#2 Quelle est l’origine du format letter ? C’est plus incertain mais selon une source internet de l’Association Américaine de la Forêt et du Papier[16] cela serait lié à l’envergure de bras maximale des travailleurs hollandais du 17e siècle. Et pourtant, ce n’est que dans les années 1980 que le format 8.5’’ par 11’’ fut officiellement adopté.
#3 Nos photocopieuses sont-elles compatibles avec les feuilles françaises et si oui le Lycée est-il prêt à nous fournir des ramettes de papier A4 ?
La réponse à celle-ci est sans doute d’essayer d’utiliser de moins en moins de papier…
———
[1] #whitecrow #winterhascome #thekinginthenorth
[2] Pour plus d’informations sur les températures, voir la Chronique du Matheux Chapeauté #4 à l’adresse suivante https://life.lfny.org/2013/08/29/the-math-hatter-chronicle-vol-2-no-1/#
[3] A la télé bien sûr car non seulement les matches les plus proches des équipes locales (Giants et Jets) ont lieu dans le New Jersey mais surtout en raison des tickets un peu onéreux, notamment par rapport aux résultats récents de ces deux équipes.
[4] Et si vous ne pouvez vraiment pas résister à l’envie de convertir, sachez qu’un pouce correspond à environ 2,5 centimètres et que par conséquent 1 pied mesure 30 cm et 1 yard 90.
[5] On se calme les fans des Yankees. La première partie de ce texte a été écrite au mois de juillet au moment où personne ne leur donnait la moindre chance mais maintenant que les “baby bombers” sont arrivés, il y a encore un peu d’espoir.
[6] En raison de l’influence américaine à travers le monde, d’autres pays utilisent le format letter parfois couplé avec d’autres.
[7] Si vous essayez avec un cube (ou un quelconque objet 3D) le volume du cube agrandi sera 8 fois plus grand.
[8] L’unité n’importe pas ici puisque c’est le ratio qui nous intéresse.
[9] Histoire très riche trouvée ici : https://www.cl.cam.ac.uk/~mgk25/iso-paper.html
[10] Une aventure incroyable que je ne saurais raconter mieux que le regretté Denis Guedj dans ses livres « La méridienne » ou « Le mètre du monde. »
[11] https://www.cl.cam.ac.uk/~mgk25/loi-timbre.html
[12] Après avoir été complètement redécouvert indépendamment au début du 20e siècle par un autre allemand.
[13] Et pas 840 comme le suggère la méthode en raison des arrondis.
[14] Il existe en fait d’autres séries dans le système ISO 216 (pour les enveloppes notamment) mais l’idée reste la même.
[15] That’s the way the cookie crumbles.
[16] https://web.archive.org/web/20120220192919/http://www.afandpa.org/paper.aspx?id=511
About the Author :
Originaire de Bretagne, David Soquet a obtenu une maîtrise de mathématiques à l’Université de Rennes et est devenu enseignant au tournant du millénaire. Après avoir affuté ses compétences au collège de Chantilly, près de Paris, il a été recruté par le Lycée en 2008. Père de deux enfants, David est aussi passionné d’histoire des sciences et essaie de contrebalancer la rigueur essentielle à l’enseignement des mathématiques avec l’humour et une invitation aux découvertes. Sa propre curiosité l’a aussi amené à s’intéresser à des sujets aussi variés que l’origami modulaire, la mythologie nordique, le cinéma de Fritz Lang et la musique.