So you thought you’d go away for the summer to try and avoid New York’s heat. I don’t blame you. It can be quite unbearable sometimes with that humidity which would have you believe you’re walking in the rainforest. Personally, I stayed in Manhattan and survived that crazy weeklong heatwave in July. One for the books. But after that, believe it or not, we haven’t had one single day in the 90s. We had some very humid days, which felt hot, but temperatures remained in the low 80s. It might be a first, too, for August.
I know what I’m talking about as I’ve spent more than half of this century’s Augusts here. My first one was back in 2001, the first summer of the century(1). I remember walking along Fifth Avenue and entering stores just to get some cool air. The difference was incredible, just like the contrast between the train and the platform in the subway — something which always comes as a surprise to someone used to Parisian public transportation. I still recall one particular jewelry store whose AC was broken. It was so hot that customers were coming in and going out right away. The owner had to sell everything 50 percent off. I married here that summer in late August, about a week before starting my first year as a certified teacher. I like to say I’m a teacher of the new millennium.
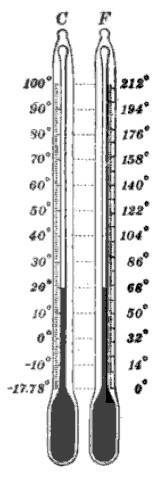
Anyway, one thing I have noticed since I’ve been working here is that a lot of French people in LFNY community never adapt to the Fahrenheit scale of temperatures. In other words, temperatures in the 90s don’t mean much to them, they need the “translation”, which is above 30° Celsius. Of course the same can be said about Americans who visit France and that is completely understandable. When one is used to a system, one resists change. The same goes with the different units of length or weights, even though in that case one system is much better than the other. Just ask sixth graders if they’d rather convert their height of 1.45 meters in centimeters or the equivalent 4’9’’ into inches.
As another example, I have a big bar of chocolate which I bought this summer and because it is imported directly from Belgium it weighs exactly 500 grams, something a French person can easily imagine because this is as much as 5 regular chocolate “tablettes”. But, to an American connoisseur (of good chocolate) used to weights of 4, 8, 12 or 16 ounces, the equivalent 17.6 ounces written on the package might seem confusing, especially if she or he tries to figure out the weight of one of the 40 squares. Right there you might think, “who in his right mind would bother to calculate the weight of one chocolate square ?” I assume you mean “Besides a math teacher who is short of ideas for a test,” right ? Well, what if you want to make a cake and all you’ve got is a french recipe requiring 75 grams of chocolate ? Well as 500÷40=12.5, you would need exactly 6 squares. I hear you, “that’s what kitchen scales are made for !” But if you have a scale why do you even come and bother me about converting your weights ? Seriously, don’t interrupt anymore. I’m barely half way through this thing and I didn’t even want to speak about grams and ounces in the first place.
By the way, because 17.6 ounces is exactly one pound plus 10 percent, the store had the idea of calling the bar “Pound plus”(2). And speaking about the pound, I very recently learned (and can’t help wikisharing it with you) that its official name is the avoirdupoids pound. As you might guess, it comes from the French, or more precisely the Anglo-Norman French and now has an official corresponding weight of 453.59237 grams. But what is interesting about the history of the pound is that there were several different other ones such as the Tower pound, the London pound or the Troy pound, which are not used anymore. The Troy pound (with a value of 12 Troy ounces or about 373 grams) was used by jewelers to weigh precious metals and actually offers an unsuspected explanation to the famous riddle “What weighs more, a pound of feathers or a pound of gold?” (3).
But back to temperatures. I believe one of the reasons very few people master both the Fahrenheit and the Celsius scales is that there is no easy way to switch from one to the other. You may have heard of some formula such as “multiply by 9, divide by 5 and add 32”. This is not so hard to remember and with a bit of practice you may discover that dividing a whole number by 5 is quite manageable. Still, working this out everytime you want to switch from Celsius to Fahrenheit is far from convenient. The problem of course is that the scales are not proportional one to each other. If you’ve been to France for the summer you may have needed to change your dollars into euros. For each 100 dollars you should have received about 75 euros. If you double the amount in dollars, you also double the amount in euros. All you need is one number to switch from one currency to the other. That’s proportionality for you. That’s easy. And if you have no dollars, you have no euros. But it doesn’t work like this for the temperatures. If you have 0° C you don’t have 0° F but 32. Is it hopeless ? Well, of course, you could always use your smartphone app which can convert anything into anything. But there is an easier way, and to get to it, I need to explain a few things first. It shan’t be long.

As I have said, the two scales are not proportional. However there is between both quantities what mathematicians call a linear relation. What it means is that if you make a graph with the temperatures in Celsius on a horizontal axis and the temperatures in Fahrenheit on a vertical one, then all the dots assigned to the couples of coordinates corresponding to the temperatures in the different scales (as (0;32) for example) will be positioned on a straight line(4). Any scientist who gets a straight line from an experiment is happy because it offers a very simple kind of regularity and it means there is an easy way(5) to switch between quantities. Here is how it works graphically. Choose any dot on your line. If you haven’t drawn it yet, you don’t actually need to plot all the dots by using your smart app. You only need two, and I already gave you one so all you should know is the fact that water boils at 100° C and 212° F (6). There you go. From your chosen dot, move 10° C horizontally to the right and then move straight up until you reach the line again. If you did it right, you increased the temperature by 18° F. Do it again : 10° C to the right makes 18° F up, 10° C to the left makes 18° F down. To each variation of 10° C corresponds a variation of 18° F. In other words the variations are proportional. If we start at (0;32), we get (10;50) then (20;68), (30;86)¸ (40;104) all the way up to (100;212). To quickly evaluate most temperatures, it is a good idea to memorize these first five couples and if you need more precision, you can raise the temperature by increments of 5° C and 9° F. So let’s say that one morning the forecast is 74° F. You know that 68 is 20, so 77 (68+9) is 25 (20+5). That means 74 should be about 23. But for most people, knowing it is between 20 and 25 is enough to decide if they’ll need a sweater. For the winter, you substract and go down (-10;14), (-20;-4) etc… Finally, in order to bake your chocolate cake, you should now easily be able to figure out that 200 ° C is a bit less than 400° F.
I’ll conclude with a riddle. Two explorators, an American and a French, worked together on a 19th century expedition(7). At one particular moment, they decided to check the temperature, and O surprise ! Both thermometers showed the same exact number although they were using a different scale. Were the two explorers wearing a light colonial hat or a heavily furred chapka ? If you’ve payed attention, it shouldn’t take you more than a minute.
(1) Yes, the 21st century started on January 1st, 2001 not in 2000, the reason being there never was a year 0 in the julian calendar.
(2) They come with whole almonds in bittersweet or milk chocolate. If you want to know where to find them, just email me.
(3) It does not work with the French version « Un kilo de plumes ou un kilo de plomb ? ». One kilogram is one kilogram.
(4) If you do that with the dollar/euro relation, you will also get a straight line but that one will go through the dot with coordinates (0;0) which is called the origin of the graph. This is a sure sign of proportionality.
(5) The technical term here is funtion but it won’t be necessary to go into this.
(6) Under normal conditions of pressure, as a science teacher would tell you.
(7) Both scales were invented in the 18th century by the German physicist Daniel Gabriel Fahrenheit in 1724 and the Swedish astronomer Anders Celsius in 1742.
About the Author :
Originally from Brittany, David Soquet graduated from the Université de Rennes, before becoming a math teacher. After honing his skills at a middle school near Paris, he joined the Lycée Français in 2008. He is the father of two children and is passionate about the history of science. In his teaching, he tries to balance the rigor required by mathematics with humor and discovery. He is very curious and his interests range from modular origami and norse mythology to Fritz Lang’s cinema and music.


