In a recent episode of Game of Thrones (Season 5, Episode 2) the men of the Night’s Watch vote to decide who shall be their 998th Lord Commander. No spoiler alert, you can keep reading! This is not the place where you will learn that Jon Snow is killed in that second episode [1]. The proud and courageous men, famously dressed in black, have to choose between three candidates by throwing in a bag a token of a certain shape: a circle, a triangle or a square. If this system seems rudimentary, let’s just say that voting machines don’t always guarantee a better result; you may remember a certain important election at the end of the last century [2]. And as we will see, the way people vote (raised hand, paper, electronic etc…) is usually less important than how the vote is processed (one or two rounds, proportional or not…). In the series, there is only one round, and after all tokens have been gathered and piled up on what looks like a tower of Hanoi game set [3], there is a tie between two candidates, the third one being far behind with only 5 or 6 votes. In the end, it is only when Maester Aemon adds his own token that a winner is declared.
“Tower of Hanoi 4” by André Karwath aka Aka – Own work. Licensed under CC BY-SA 2.5 via Wikimedia Commons.
This leads to an interesting question: what would have happened if there had been a second round ? After all, many elections are done with two rounds, using the (in)famous rules of absolute majority and simple majority, and it is the organizer of the elections who has to decide first which procedure shall be used. For example, at the Lycée, the election for the Conseil des élèves is decided with a single round, while a two-round system is used for class delegates, as decided by the administration. In the latter case, another decision has to be made before proceeding to the second round. Should the candidates with the lowest scores in the first round be eliminated ? As you know, for the French presidential election, only the two candidates who receive the most votes in the first round can continue in the second round. In other cases, any candidate who gets a predetermined minimum number of votes qualifies for the next round. In our school, all candidates remain in the second round unless they willingly withdraw.
Voting on the colors allowed in the LFNY dress code
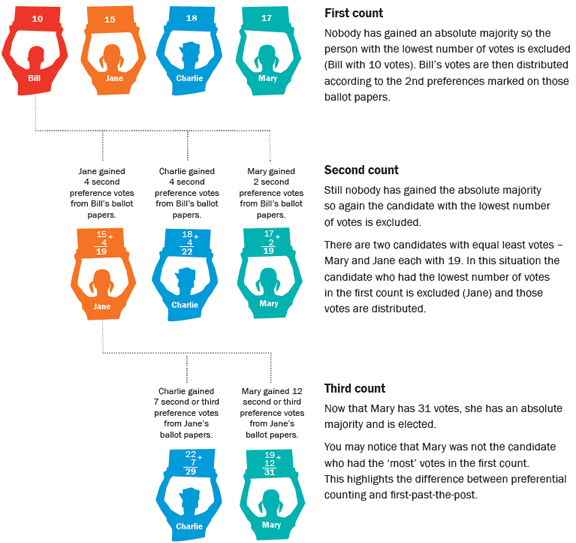
So what would have happened in GOT ? Let’s try to break it down. If a man voted for one of the top two candidates, he has no reason to change his vote in the second round. However, if he voted for the third candidate, whether or not the rules eliminate that candidate, he should of course change his vote. The results of the first round taught this voter one piece of information:his favorite candidate has no chance to win. Therefore, if he wants to have an impact on the final outcome of the election he must vote for one of the other two. We have no way of knowing if the 5 or 6 votes which were given to the candidate who came in last would have changed the final result in a second round, but we know they had the potential to do so, the difference between the two leading candidates being only a single vote. Of course, if a voter doesn’t care which one of the two wins, he might as well vote again for his candidate or cast a blank ballot if he was eliminated by rule. But if one of the two other candidates is his sworn enemy, or if he has even the slightest preference for one of them, then he should change his vote. This illustrates the importance of the two-round system.
Illustration of the concept of absolute majority.
This is where the concept of absolute majority comes into play. Basically, it means that even if all your enemies conspire against you, you would still get more votes. Let’s look at an example. Imagine that the CPET decides to add a new color to the limited dress code palette and asks the student body to choose between orange, red and black. From MS to Terminale, everyone will vote and, according to conversations overheard in the secondary, it seems that black might win in a landslide. But after a cautious double count, the results come as a bit of a surprise: black gets 48% of the votes, red 34% and orange 18%. It is possible that some students voted for a fourth color or abstained, but, according to the rules, those votes are discarded and not included in the count.
Red vs. black
So what happened ? Well, not surprisingly, orange came in last, being such an ugly color. But more importantly, black came short of having more than 50% of the votes, or as it goes “half the votes + 1”. It received only the “simple majority”. Apparently, contrary to the pre-election forecast, some students feel that dark gray (a color allowed at the Lycee) is close enough to black. It is true that nobody knows more shades of gray than a LFNY secondary student. Had it been the election for “conseil des élèves” black would have won but for a decision as important as this the CPET decided it should be an absolute majority. That means that a second round is necessary and of course everybody can guess what will happen. The students who voted for orange, whether or not their first choice was removed from the options for this new round, are true color lovers and will do whatever they can to keep black from winning.. Each one of them switches their vote to red and the results of the second round are black 48% and red 52%. This means that red is the winner despite being far behind black in the first round.
This, of course, is an oversimplified example and at least two criticisms could be made. First, there is no guarantee that red will recuperate all the orange votes between the two rounds. It is possible that some orange voters will lose interest in the election and decide to cast a blank vote or abstain. Then, turning the point around, it is also possible that some overconfident supporters of the black color didn’t show up for the first round (or voted green) because they thought black would win easily. Now, seeing that red has a chance to emerge victorious in the second round, they come in throngs to the polls to ensure that black wins.
People “vote with their hearts” for the first round and “vote with their heads” for the second one
This is the whole point of the two round system. It is sometimes said that people can “vote with their hearts” for the first round but should “vote with their heads” for the second one. To allow this, one crucial element is needed: the results of the first round must be made public. To go back to our example, if the results of the first round had not been announced, the students who voted orange would have had no way of knowing that their favorite color had literally zero chance of winning. They then would have voted for it again in the second round (as the other voters) and ended up having no impact at all on the final result. Black would have been elected with 48% of the votes.
This is where a recent decision of the administration intervenes. For this year’s class delegate election, here is what advisors were asked to do :
– If a candidate receives the absolute majority, announce the winner to the class.
– If not, tell the class that we will proceed to the second round without giving the scores.
At first glance, it is clear that this decision was made to protect the candidates’ self esteem. Indeed, when the number of candidates is large, it is not rare to see one candidate receive a very low number of votes, sometimes only two or even one. And if you’re thinking : “How can one candidate get only one vote if he runs as a “tandem”, including one delegate and one deputy ?” the answer is actually quite simple. It turns out that students are allowed to be part of two or more tandems, as a delegate or as a deputy. And of course they give their single vote to themselves. Of course it is not very pleasant, especially when you are a young middle schooler, to discover that none of your classmates voted for you. Still, some would argue that if someone steps into the spotlight by running, he should be able to face the public opinion. After all, nobody was forced to run. As we saw before, the problem with not disclosing the results is that the poor candidate will vote for himself again, unaware that this will be his single vote, whereas he could have used that knowledge and his vote to make a difference in the final result by voting for his “second choice”.
One solution to solve this problem and avoid the “humiliation” of candidates would be to keep only the two highest scores for the second round. This wouldn’t require the disclosure of the results. Our unfortunate candidate would not be delegate that year but people may still think he was close.
Primary school students vote for their class delegates in November 2014.
Until recently, there was another issue with elections at the Lycee. Now that the advisory program has been generalized to all grades, each advisory group gets to elect its own delegate, but before that, a whole class was electing two delegates at the same time. This led to a serious problem regarding the definition of absolute majority. Let’s see why by considering a class of 24 students, each one of whom could write down two different candidates (or two tandems) on his ballot. This meant we had 24 voters with 48 votes.
If the absolute majority was defined as “half the votes +1”, it meant a candidate would need 25 votes to be elected in the first round [4]. But since a candidate could not receive more than one vote from each voter, this was clearly impossible. So instead it was decided that the absolute majority would be “half the voters +1” (13 in our case) which led to this completely different problem: because 3*13=39 is less than 48, it would be possible for three different candidates to get the absolute majority. With a bit of algebra, it is quite easy to show that the risk is higher when the number of voters increases – it’s no surprise that this actually happened a few years ago, when about a hundred terminale students voted for the “conseil des élèves”. At the time, it was still an election in two rounds. This was the event that prompted the dean to change the system to a single round. However, the procedure for class delegates was not changed, and this year is the first time that this issue won’t arise anymore because each tandem’s election is independent.
There are several possible solutions to this problem. The first is to do two separate elections, one for each delegate, which poses the inconvenience of prolonging the process and giving more legitimacy to the first elected candidate because he was the first choice of more students. This is actually a non-issue because the old system allowed everyone to see who was getting more votes anyway. I remember one year when there were only two candidates in my class, which made the whole process of voting quite futile. The first delegate was elected with an absolute majority and the other won the second round with four votes out of 20 because he was the only remaining candidate. Talk about representation!
“Majority of the two-thirds”
Another solution is to allow the students to give their two votes to the same candidate, thus making it possible for a tandem to get more than 25 votes. It would be interesting to see if they would decide to ensure the election of one of their choices or try to elect two. Finally, a more mathematical solution consists in using a different absolute majority by requesting more than two thirds of the votes, 17 in our example. Because 17 is smaller than 24 it would be possible for a candidate to be elected in the first round and it would also avoid the other problem because 17*3=51 is greater than 48 [5]. This “majority of the two-thirds” is used in many elections around the world.
Secondary class delegate elections in October, 2014.
Election problems are not new and choosing the best system is not an easy matter. In the second half of the 18th century, the Marquis de Condorcet [6], a French politician, mathematician and philosopher, understood that very well and proposed a method to try and get the fairest result. To explain it in a simple way, let’s reconsider our dress code example and add a fourth color to the mix. Students now have to choose between black, red, green and, yes, that awful orange again. The first thing Condorcet proposed was to ask the voters to rank all four colors in their order of preference instead of selecting just one. So let’s imagine our results are the following [7] :
– 42% of voters put black first followed by green, orange and red.
– 26% go green, orange, red and black.
– 15% prefer orange and then red, green and black.
– 17% put red in first position, then orange, green and black [8].
Using a single round with simple majority system once again gives an easy win to black. No surprise here. But let’s see what happens if an absolute majority is required. First, we should eliminate the candidate who arrived last. There goes orange. Now, the great thing about the ranking is that we don’t even need to vote a second time, we can simply reassign the 15% of votes who had put orange first to their second choice which happens to be red. This means that the new results are 42% for black, 26% for green and 32% for red. Once again, there is no absolute majority so we eliminate green and reassign its votes to…red, the next choice. In the end, red gets 58% (versus black’s 42%) and is therefore the winner. This method, called “instant runoff voting”, is used in many countries: to elect the members of the Australian House of Representatives, the President of India, of Ireland, and for some local elections in the United States.
However, with the system used for French presidential elections we would keep only the top two scorers, black and green, and once again all the other votes would be assigned to their next available choice. Green would get the 58% and win the election.
Different voting systems lead to different results
In other words, using three different systems, we got three different results. Condorcet thought this was a problem and he proposed another method. He said that comparing all the candidates head to head was the only sure way to get a fair result. If we apply this to our example we find that 58% put green before black, 68% put green before orange and 68% put green before red. According to Condorcet, because green wins all the matchups, it should be the winner [9]. I’m sure nobody would argue with that but one problem with this method is that it can sometimes lead to a stalemate, a situation foreseen by the Marquis and called Condorcet’s paradox.
Imagine a situation with three candidates A, B and C where you know that 2/3 of the voters prefer A to B and 2/3 of the voters prefer B to C. You might want to conclude that A should be the winner, but that would be a grave mistake because it is entirely possible that 2/3 of the voters prefer C to A. Here is how : 1/3 say A > B > C, 1/3 say B > C > A and 1/3 say C > A > B. As you can see, A beats B in two of the three matchups. But the same goes for B against C and C against A. Who should be elected ?
These examples are of course theoretical and one would be unlucky to encounter such a situation. Still, it proves that no system is perfect and even Condorcet’s method had its detractors, the first one being Jean-Charles de Borda, another French mathematician. Contemporaneous of Condorcet, Borda proposed to use a system of points : 4 points for 1st place, 3 for 2nd place, 2 and 1. With that scenario, black would get 42*4+58*1=226 points, green 26*4+42*3+32*2=294, orange 207 and red 273.
Green would be the winner again but it is possible to find an example in which the Condorcet and Borda’s methods don’t yield the same result. I leave it to the reader to come up with one. Then of course, one could argue that more points should be given to first place because this is the candidate each voter wants to have elected but these are only details which have to be agreed upon beforehand. Once the rules are written down, everyone understands the importance of his vote and can vote accordingly.
The downsides to the electronic vote
In conclusion, we see that organizing an election is not a simple matter because decisions regarding the process we use can have a serious impact on the results. If we want to educate our student community about the values of democracy and citizenship, we need to ensure that they understand the election process and how (and if) their votes will be counted. The recent implementation of the electronic vote has also had consequences. The fact that the votes are no longer counted one by one in front of everyone has removed the suspense and excitement about the results. But we also lost something more important: because the computer only gives the results as percentages, which are calculated without counting blank votes, we can’t know how many votes the winner received. If there is only one candidate in an advisory group (something that happens quite often), not only will he be elected in the first round but he will also be elected with 100% of the votes, even if he gets only one. We need all participants to understand this, so they can make an informed choice.
(1) Sorry I meant to write « if ».
(2) For those of you who may be confused, let me remind you that this century started on January 1st, 2001.
(3) I think that system is interesting because it is a very visual way to see who is the winner.
(4) Depending on the elections, absolute majority can also be calculated with the valid votes only, meaning the blank and null votes are not included.
(5) Again, a simple generalization proves that this solution (by far my favorite) works for any number of students.
(6) A.k.a Marie Jean Antoine Nicolas de Caritat, or simply Nicolas de Condorcet.
(7) Numbers taken from a wikipedia example.
(8) Other combinations are of course possible but this would only make the whole thing more complicated without changing the conclusion.
(9) It can be easily checked that orange beats red and black, red beats black and black loses each matchup despite having the best score for first place.
About the Author :
Originally from Brittany, David Soquet graduated from the Université de Rennes, before becoming a math teacher. After honing his skills at a middle school near Paris, he joined the Lycée Français in 2008. He is the father of two children and is passionate about the history of science. In his teaching, he tries to balance the rigor required by mathematics with humor and discovery. He is very curious and his interests range from modular origami and norse mythology to Fritz Lang’s cinema and music.