Upon arriving at the Lycée, there are a few things a French teacher needs to adapt to, and I’m not talking about the seven-day schedule because that novelty is not exclusive to French teachers, nor new teachers for that matter. No, what I’m thinking about are these small details which are an integral part of the American way of life – such as the double symbolism of the apple for a New York teacher – and I will try to review some of them here.
First, there is of course the Fahrenheit scale of temperatures and I guess arriving in New York City in the middle of the summer is a perfect way to understand right away what “Temperatures in the 90’s” mean, even though that won’t make it less surprising when these temperatures go down to 0° Fahrenheit and you start feeling the “Winds of Winter”[1]. Then, once you’ve familiarized yourself with this[2], another important thing to tackle is the non-metric system and –let me warn you here– that one is much harder, so hard in fact that you might think it would be easier to try and convince Americans to switch than to learn their archaic and incongruous system. And yes I mean those words. This is one of many paradoxes of this country, capable of incredible achievements (#RioOlympics) and at the same time having yet to implement the equivalent of the “Navigo pass” in the metro or put in place a sound and logical voting system, as you will certainly notice in a couple of months. For sure, you might be a bit hopeful after your first conversion from square feet into square meters but the truth is that you are usually left with that familiar comment “Oh yes, my UES studio is small!” Let me be honest with you, converting won’t help. For that kind of problem, I recommend total immersion.

But you’re in luck. It turns out that just two days after the first day of school is the official start of the NFL season and I believe there is no better way to learn about yards, feet and inches than to watch a game of American Football[3], the sport which arguably has the highest I-like-to-watch-it/I’d-like-my-kids-to-play-it ratio among the most popular sports. Even if you don’t understand all the rules right away, it will at least give you an overall understanding of the common human scale units of measurement and if you want to know more you should just remember that 1 yard is 3 feet and 1 foot is 12 inches[4]. As an extra, it might also help you understand the conversations of some of your students or colleagues on Monday mornings.
Come October, when the NBA season starts, you should be familiar enough with the system to understand that if most basketball players are between 6 and 7 feet, you are probably between 5 and 6. Finally, if you’re curious enough to try and watch baseball –that other iconic American sport– October is playoff season and even if you will most likely not get to see any Yankees’ game because they will most probably miss the postseason[5], seeing a fastball zip at close to 100 mph will give you an idea of the speed unit used here, maybe not a very precise one but certainly better than trying to understand how fast is the 25 mph limit by riding a yellow cab.
If I’m having a bit of fun with this it is because these difficulties may end up being minor ones as compared to this other unexpected one which could bother you on a daily basis: paper format. As you will soon discover when you start using the printer and copy machines, the paper format in the US is different than the one used in France. To be more precise, out of almost 200 countries in the world, only 3 don’t use the format French teachers are familiar with: Mexico, Canada and the United States[6]. As I will explain in more details later, the traditional A4 page measures 210 millimeters by 297 millimeters (or 8.27 by 11.69 inches) while the common US page – which is called letter – measures 8.5 by 11 inches (or 216 by 279 in mm). In other words, the US page is 6 mm wider but 18 mm shorter. It doesn’t seem much but, as we will see, this slight difference has some consequences which range from minor to really painintheneckesque and which are also interesting from a mathematical point of view.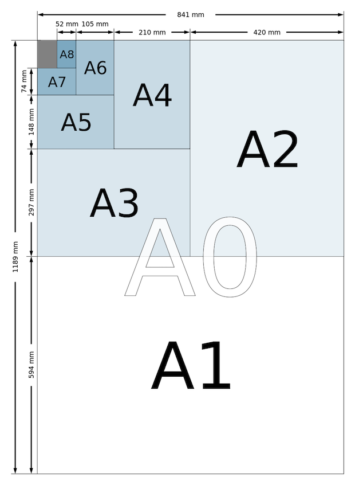
Let’s start with the minor ones. First, in case you were wondering, some of your students will use US papers and others will use French ones and when you will gather them after a test or any type of written work they will be mismatched. The US test paper will come out of the side of the French “copies doubles” – a word which should not be translated as I still have to see the equivalent here – and these will be longer than the rest. Of course you could foist a paper format on your class but you may discover that American users of the (in)famous yellow letter pads resist change, especially when you can get a dozen of those for the price of one pack of Clairefontaine sheets. You’ll get used to it. Now let’s speak about your documents. If you brought a lot of paper copies of them from France, you have perhaps figured out that you won’t be able to copy them for your students “as is” because there is no A4 paper at the Lycée. Get ready to reduce them (I suggest 93%) or lose your titles! And if you think you’re good because all your files are in digital format, think again! Chances are your word documents were saved in the A4 format, and it means you will have to switch to the letter format in your page layout. It seems simple and it’s actually not so bad if your document is made mostly of text and doesn’t have references depending on page numbers. However, if it contains images, graphs and several titles it can be very frustrating to try and rearrange everything, especially if you like to have something very neat.
All right, now that I have mentioned the need to reduce documents, I believe it is time to ask one crucial question. Why is the system of paper formats used in France (and almost everywhere else except in North America) so much better and how was it achieved? To explain this I first need to speak about film cameras and scaling. It may seem odd for most of our students, but there was a time when a phone and a camera were two different things, a time when one had to load up “film” in a camera to take pictures and bring that film to a store before one could see any photos. I was reminded of that in a funny way recently when my daughter had her first overnight trip last Spring, and she was allowed to bring a disposable camera. I personally thought these things didn’t exist anymore but we eventually found one in a local drugstore, to my daughter’s delight. I explained how it worked, and when she returned after three days of splashing discoveries she said she may have taken only 2 or 3 pictures but was not sure it had worked because she may have forgotten to rewind the camera each time. Then, a few weeks later, I decided I would use the remaining 20+ pics during my son’s kindergarten graduation ceremony and following picnic. And right after I took a picture of him with his best friends my son asked “Can I see it?, a reflex he’s had for years each time I’ve been taking pictures of him with a digital camera.

It turns out that the pics were pretty bad – especially the ones with the lousy flash in the auditorium – but at least one of them was worthy of being framed and gifted to Grandma. Before that it would need to be enlarged, and this is where the mathematical notion of “scaling” comes into play. This may seem obvious to everyone but when you wish to enlarge (or reduce) a picture, you need to do it along its two dimensions if you want your picture to have the same aspect ratio. If you do it along only one, your kid’s face will look flattened as reflected from a deformed mirror. The ratio of a rectangle is simply the quotient of the length by the width and is sometimes expressed with the two numbers as with the aspect ratios 4:3 and 16:9 of TV screens. Obviously, if you double the length and the width of your picture, the ratio remains unchanged and a simple consequence of this is that its area will not be doubled but instead 4 times bigger. If you don’t see it, draw any rectangle, double the lengths of its sides and you will see that the new enlarged rectangle can fit four samples of the original one. This is true for any 2D shape, be it a triangle, a polygon or a circle[7]. If you enlarge or reduce all lengths by a factor k (meaning you multiply them by the number k), the area will be modified by the square of k (k2 or k×k). That is why there are 100 square millimeters in a square centimeter. That’s not rocket science, but it leads to a very interesting problem which I submit to you now:
Draw a square and, without any calculations or measurements, draw a second square whose area is exactly twice the area of the first square.
As simple as this very old problem looks, it is possible that you won’t find the answer right away so feel free to stop reading and focus on it or keep reading and try to solve it after you’re done. I’m not giving the answer anyway.
The problem with a square – and with all squares – is that its ratio is of course 1 and however you enlarge or reduce it, it will remain 1. We already know that doubling the sides of the square (an enlargement factor of k=2) won’t work because the area will be 4 times bigger. What about one and half longer? Well 1.5×1.5 is 2.25 and it is still too much. I’ll let you check that 1.4 is close but not enough. You guessed it! We’re actually looking for a number k which solves k×k=2. And as you may remember, that is the exact definition of the square root of 2 (written √2) whose value is about 1.41421356237… And no this doesn’t give the solution to the problem because remember you can’t calculate or measure anything. You have to find a geometrical way to double the square. But the square root of 2 is the mathematical link to our paper format problem.
Let’s go back to a rectangular piece of paper and let’s take 1 for the short edge and √2 for the long edge[8] which of course gives us an aspect ratio of √2. Now let’s put two samples of this paper next to each other along their long edges to obtain a larger rectangle with double area. The dimensions of this new rectangle are √2 and 2 and the new aspect ratio is √2 again because 2 divided by √2 is √2. In other words the second rectangle is an enlargement to scale of the small one. Finally let’s take one copy of our original rectangle again but this time let’s cut it in half along the longer side of √2. We get a smaller rectangle whose dimensions are now 1 (the intact width which now becomes the length) and half of √2 or √2/2 for the short edge. To calculate the ratio of this new rectangle we need to divide 1 by √2/2. I don’t know how much you remember about division by a fraction but – and I ask you to trust me or your calculator on this one – the result is again √2 and this means that the small rectangle is a reduction – again to scale – of the first one.

This nice property of the number √2 – which is shared by no other number – was noticed by the German scientist Georg Christoph Lichtenberg in 1783[9] and it soon inspired the French revolutionists who, after creating “le mètre” and all its derivatives (including “le litre” and “le kilogramme”) in 1793[10], passed a law called “La loi sur le timbre”[11] which defined how paper should be taxed and what sizes should be used. One can actually see that the size named “Moyen papier” corresponds exactly to the format known today as A3 and whose dimensions are 420 mm by 297 mm. If you remember the numbers I gave earlier you will notice that this is obtained by putting together two A4 pages (297 by 210) and this is actually how this system – the international standard which today is called ISO 216 – works[12]. Put two A3 pages side by side and you get the format A2 (594 by 420) which then gives A1 (841[13] by 594) and finally A0 (1189 by 841). Now cut an A4 page in two and you get the format A5 (210 by 148) etc… all the way to the tiny A10 which is 37 by 26.
There you have it! If you put two A4 pages in a copy machine you will get an A3 page. And here the Americans go “Duh! If I put two pages in the letter format (remember 11” by 8.5”) in the machine, I get a page whose dimensions are 17” by 8.5” which is exactly the US paper size called ledger. I don’t see what’s so special about your system.” They are absolutely right and this is why the other type of paper you will be able to select at the Lycee is the 17” by 11”. Except that… Except that I have a question: what happens if I only have one page and I want my copy machine to make it bigger on another paper format, just like my son’s photograph?
Well, it is possible that you missed the link between Lichtenberg’s ratio of √2 and the French paper formats because I didn’t ask you to do the calculations. Let’s do them now. For the A4 we get 297/210≈1.414, for the A3 it is 420/297≈1.414. I’ll let you do the others to check that all the paper formats in the A series[14] have an aspect ratio of √2. This is not surprising because, as we saw before, if the first one has this ratio then all of them have the same because of the way they were designed by doubling or halving one edge. And this is the fundamental part. When you enlarge or reduce a document, the new one will have the same ratio. This means that your A4 picture, once enlarged, will fit perfectly on an A3 page. Or let’s say you have two A4 pages of your lesson which you want to fit on one single A4 page before making copies for your class because your school has a “Go green” policy. In France you put both pages next to each other on the machine and hit the button “A3 to A4”. No content is lost and no blank parts appear.
This won’t work at the Lycée. Why? Simply because the aspect ratios of the two most used paper formats are not the same. For letter format it is 11/8.5≈1.294 and for ledger it is 17/11≈1.545. As they say here, this is the way the cookie crumbles. If you want to enlarge a letter page to fit on a ledger page no simple button will do. You will have to specify how much bigger you want it, and you can’t use an enlargement factor bigger than about 1.3 (or 130%). The result will be a page of dimensions 11.05” by 14.3” and this means you will have almost 3 inches of lost space on your page. The other way around, trying to reduce two letter pages to fit on a single one you will have to cut it to 65% to have your 17” length fit on 11”. The consequence of that reduction on the width is a blank space of 1.35” all along. And if you want to avoid the blank space and decide to reduce your document to 77% of its original size, its length will be more than 13” and you will lose 2 inches of content. There is just no way around because as we saw, scaling has to be uniform if you don’t want your pictures to look weird. This truly illustrates the incredible superiority of the ISO 216 system and makes one wonder why the US stubbornly refuses to change.
Three questions remain.
#1 How were the dimensions of the A0 format decided? It’s actually quite simple. The French reformers started with a big page of 1 m2 (squared meter) and because the page needed to have an aspect ratio of √2, they were looking for two numbers a (for the length) and b (for the width) which solved the two equations a×b=1 and a/b=√2. A bit of algebra gives a=√√2 (the square root of the square root of 2) and b=1/a (the reciprocal of a). Approximate values of these numbers are a≈1.189207 and b≈0.84089 and explain why 1189 mm and 841 were chosen for A0.
#2 Where does the US letter size come from? It is less certain but an internet source from the American Forest & Paper Association[15] suggests that it could be related to the maximum distance a 17th century Dutch worker could stretch a piece of paper. And still, it was only in the 1980s that the 8.5” by 11” format was made official.
#3 Are our copy machines compatible with the French sizes and if so how willing is the Lycée to provide us with reams of A4 paper?
Maybe the answer to this one should be to try and be ever more paperless…
———
[1] #whitecrow #winterhascome #thekinginthenorth [2] For more details about temperatures you can check out Math Hatter Chronicle #4 at https://life.lfny.org/2013/08/29/the-math-hatter-chronicle-vol-2-no-1/# [3] On TV of course because first the closest games for the “local” teams Giants and Jets are in New Jersey and secondly because the tickets are usually overpriced, especially considering the results these two teams get in recent years. [4] And if you can’t resist the need to convert, 1 inch is about 2.5 centimeters and therefore 1 foot is 30 cm and 1 yard 90. [5] All right Yankees fans, the draft of this paper was written in July when nobody would give them a chance but an update is necessary and now that the baby bombers have arrived, hope remains. [6] Because of the American influence throughout the world, other countries use some US paper sizes sometimes coupled with others. [7] If you were to try that with a cube (or any 3D shape) the volume of the enlarged cube would be 8 times bigger. [8] The measuring unit doesn’t matter because we will focus on the ratios. [9] Very informative story found here https://www.cl.cam.ac.uk/~mgk25/iso-paper.html [10] An incredible story which I would in no way be able to tell better than the regretted historian Denis Guedj in his books “La Meridienne” or “Le metre du monde.” [11] https://www.cl.cam.ac.uk/~mgk25/loi-timbre.html [12] Although it was long forgotten until completely and independantly reinvented in the 20th century by another German. [13] And not 840 as the method would suggest because measurements are rounded to the closest millimeter. [14] There are other series in the ISO 216 system (e.g. for enveloppes) but the idea is the same. [15] https://web.archive.org/web/20120220192919/http://www.afandpa.org/paper.aspx?id=511About the Author :
Originally from Brittany, David Soquet graduated from the Université de Rennes, before becoming a math teacher. After honing his skills at a middle school near Paris, he joined the Lycée Français in 2008. He is the father of two children and is passionate about the history of science. In his teaching, he tries to balance the rigor required by mathematics with humor and discovery. He is very curious and his interests range from modular origami and norse mythology to Fritz Lang’s cinema and music.


