I can’t sleep on a plane. I don’t think it’s due to fear of flying because I can’t sleep on a train either or any moving object for that matter. And if you’re anxious to get on planes I guess it’s the night before you can’t sleep because, once you’re on, there’s not much you can do about it. The problem when you can’t sleep during a long flight is that you need to get busy for 6 to 7 hours. After watching one or two movies, reading a few chapters of the current book and playing a couple of games of chess, I usually end up looking at the small screen in front of me which, when turned to the right channel, gives you the flight path and informations. You get to know how fast and how high the plane is flying, how many miles are left before you reach your destination and many other vital informations. I remember I was quite excited the first time I saw that and even thought I could make a math problem out of it[1].
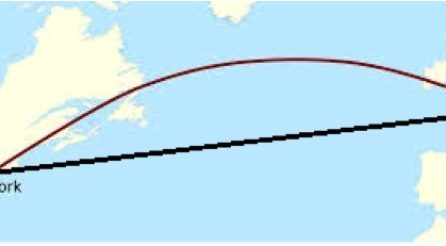
I’m sure you’ve seen it too. And if you have, you may have wondered why, on a Paris to New York trip, the plane flies north through the southern tips of England and Ireland, as shown by the red curve on the image on the right. After all, New York’s latitude is about 41° North while Paris’ is almost 49° so you would expect the plane to go south instead of reaching the Irish city of Cork, which lies at the latitude of 52°, and an even higher latitude in the middle of the Atlantic Ocean before going « down » to America. In other words, you’d think the plane would follow the string (in black) and not the bow because, as you know, the shortest way between two points is along a straight line.
So what’s happening here ? Isn’t gazoline expensive enough that you could expect your pilot to use the shortest route between Paris and New York. Well it’s actually quite simple. The reason is that we are now quite certain that the Earth is not a flat plate on the back of a giant tortoise, as an old lady once told the famous English philosopher Bertrand Russel at the end of a lecture[2]. No, it is a globe, and it means that the black line on the image is actually not straight but instead follows the curvature of Earth. In other words to go from Paris to New York following a straight line would require going through the Earth. Get ready to dig out ! This very Vernesian journey would certainly be nice, meeting a few moles on the way, but it wouldn’t be very practical.
This leaves us with another question : if no line drawn on Earth is straight, how can we determine which one is the shortest between Paris and New York ? The answer is not as simple and before anyone gets mixed up with altitude and latitude, let’s take a moment to review a few geography basics. Our globe is what mathematicians call a sphere, the equivalent of a circle but in 3 dimensions, and it means that every point on the surface of Earth is at the same distance from its center, roughly 4000 miles[3]. Of course, you might think that this is not true for the top of Mount Everest but with an altitude of about 5.5 miles it makes a difference of only 0.1%. Very negligeable. If we don’t need to consider the altitude, it means that to give our position on Earth we only need two numbers because it is a bidimensional surface : these are the latitude and the longitude.
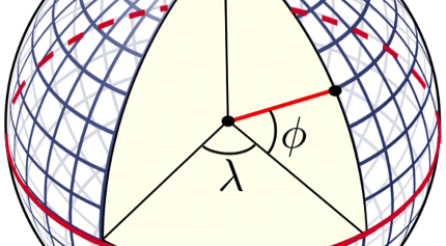
The latitude is easy. It basically tells you how high or low you are in reference to the Equator, which serves as a natural separation between the northern and southern hemispheres. Why is it measured with an angle ? Imagine a point A somewhere on the equator and draw a straight line until you reach the center C of the earth : the segment [CA] is a radius. Now starting from A again, start moving north until you reach another point which we shall name B. Again, reaching towards the center C gives you another radius : [CB]. The angle in C formed by the two radii [CA] and [CB] is the latitude of point B. It goes from 0° if you stay on the Equator up to 90° at the North Pole[4]. Of course you can also move south and that is why latitudes range from 90° South to 90° North. In addition, each location on Earth belongs to a circle whose center is on the poles’ axis and because these circles never intersect each other (nor the Equator) they are called parallels. Examples are the two tropics who are situated at a latitude of about 23° North (Tropic of Cancer) or South (Tropic of Capricorn). New York (at 41° N) is on a parallel which is further away from the Pole than the one Paris is on (at 49° N). Makes you wonder where all this snow comes from.
Finally, before speaking about longitude, you should now be able to solve this famous conundrum.
A hunter spots a bear sleeping peacefully. He aims his rifle and shoots due north in the direction of the poor beast but barely misses it. He then walks 100 meters to the East (while the bear remains asleep) aims a second time and again shoots due north and kills the bear. What color is the bear’s skin ?
Moving on. Among all parallels, the Equator is of course the longer one and its length is the circumference of Earth or a little bit more than 40,000 kilometers. As you move to the poles the parallels get smaller : the tropics are 36,800 kilometers long and Paris’ 49th a bit more than 26,000. But as geography (drawing the earth) meets geometry (measuring the earth) we discover that parallels are not the only circles which can be drawn on the globe. We can draw a circle going through both poles and centeredat the center of the Earth. These are of course called meridians. They are an infinite number of them and each one meets all parallels. That is why each point can be simply located by saying to which parallel and to which meridian it belongs[5]. To measure the longitude we use the same method of measuring an angle which we used for latitude except that instead of moving north or south, we move west or east. But there is a problem : no meridian can serve as a natural reference as the Equator did for parallels. A choice had to be made.
In 1884[6], delegates representating only 26 countries decided that the meridian passing through the Greenwich observatory in London would serve as such a reference. French delegates were not happy with the decision and kept using the Paris meridian for 30 years. Nowadays, the Greenwich Meridian remains the O° and longitude ranges from 180° West to 180° East. With longitude and latitude, every place on Earth can be located by its coordinates such as (49°N ;2°E) for Paris or (41°N ;74°W) for New York. This is all very interesting but it still doesn’t explain why our plane is going north.
But we’re close, and to get there we just need to learn a little more about the geometry on the sphere.
As we saw, it is possible to draw a circle on the surface of a sphere whose center is the center of the sphere itself. Mathematicians call those great circles, simply because they are the longest ones. Meridians are examples of great circles on the globe but they are not the only ones. It is possible to draw a great circle sideways without passing through the poles and it is easy to understand how. For any point on Earth there exists another point which is diametrically opposed to it. It is called the antipodal point and the circle which goes through both points is a great circle. Antipodal points (or antipodes) can be fun. As an example, consider this. As I’m typing this, I’m sitting in the teachers’ lounge on the 4th floor. If I start digging straight through the center of Earth and all the way to the other side, then drop a stone in the tunnel, where will it end up ?
What do you think ? Well for starters there is a good chance that the stone will be caught by a calculovorus on its way[7]. But let’s assume, in a purely theroretical way, that’s the stone makes it through, unscathed, even after going through melting lava and the iron core of the Earth. Will it get down under in Australia ? Or will it be China, following a common belief in the United States which spread in the 70’s and actually gave the name to a type of nuclear accident named « China Syndrome » where a reactor’s radioactive contents would supposedly melt through the crust all the way down to the other side[8].
It’s not easy to try and figure it out in your head but with the coordinates it takes two seconds. Again, New York’s coordinates are 41 North and 74 West. The opposite of 41 North is simply 41 South. To find the opposite of 74 West we need to move eastward half way around the earth or 180 degrees of longitude, 74 degrees to get back to the Greenwich Meridian and then 106. There you have it, the antipode of New York is the location with coordinates (41° S ; 106°E). It means that the stone will end up its journey…in the Indian Ocean, off the west coast of Australia. Actually all the continental US land has its antipode in the Indian Ocean, which is not very surprising because 70% of earth’s surface is covered with water. Exact land to land antipodes are quite rare but there are a few approximate ones that are interesting and which you may want to remember if the subject comes up during a cocktail or another soirée mondaine. Those are : Taipei (capital of Taiwan) and Asuncion (capital of Paraguay), Montpellier (in the south of France) and the Chatham Islands (next to New Zealand), Sevilla (in Andalusia) and Auckland (again in New Zealand) and finally Beijing (capital of China) and Bahia Bianca (very close to Buenos Aires).
Now, after this lengthier[9] than I had imagined digression, let’s get our heads back up and consider great circles again. Where was I ? Oh yes, meridians are not the only great circles. We can actually prove that for any two points on a sphere there is always at least one great circle which passes through both. And there lies our answer to our flight path problem because we can also prove that the shortest way between two points on a sphere is the one following that great circle. It is called a geodesic. In other words, our pilot is trying to fly along the great circle connecting Paris and New York and this is actually the red bow line on the first image.
Geometry can be tricky. The problem is that most of the stuff we learn in school deals with the geometry on a flat surface or what is called euclidean geometry from the greek mathematician Euclid who put everything together in The Elements, back in -300. And as Albert Einstein once said : « When a blind beetle crawls over the surface of the globe, he doesn’t realize that the track he has covered is curved. »
Of course, we don’t live on a flat surface but most of the time we can act like the beetle and pretend that we are. It’s all a matter of approximation. When Pythagoras was drawing in the sand he could verify that when a triangle had a 90° angle, the square of the hypotenuse was the sum of the squares of the other sides. But let’s take an even simpler example. Imagine you are in the middle of the Saharan desert and draw a small triangle. If you measure the 3 angles and add them up you should get 180°, a confirmation of the result I’m sure you remember : « The sum of the 3 angles of any triangle is equal to two right angles ». But what if you draw a bigger triangle ? Or let’s say you climb back in the jeep and drive in a straight line for one mile, turns 120 degrees to the left and drive another mile. Finally you turn 120 degrees left again and finish your trip with another mile. Where are you now ? Well, on a flat surface you would arrive exactly where you started with your tracks forming a nice equilateral triangle in the sand : 3 sides of 1 mile each and three angles of 60 degrees. But in the desert each side of your triangle is a little bit bent by the curvature of Earth and as a consequence the 3 angles will measure a little bit more than 60°. Hard to imagine ?
Well it’s true he difference would still be negligeable but nothing stops you from making a bigger triangle. Start at the South Pole and follow a meridian until you reach the Equator. Now go along the Equator at will and when you’re ready, go « down » along another meridian until you’re back at the South Pole. You made another triangle and since I’m sure you will agree that all meridians are perpendicular to the Equator, your triangle has 2 angles of 90°. It means that the sum of the three angles will be more than 180° and if you had gone along the Equator for 90° of longitude you would have encountered the poster child of spherical geometry : a triangle with three right angles.
If Euclid had ever imagined such a triangle, he may not have called it a triangle because, after all, the sides are not really straight lines. But, in retrospect, it is interesting to think that at the time The Elements appeared and Euclid explained the foundations of all geometry on a flat surface, scientists already knew that the Earth was round as illustrated by Eratosthenes’ measure of its circumference[10]. Actually, the history of spherical (and other non-euclidean geometry) is interesting because it evolved from an attempt to prove one of Euclid’s postulate :
« Given a straight line and a point outside of that line, there is only one other line which goes through that point and is parallel to the first line. »
Known as the « parallel postulate » it went unchallenged for many centuries simply because it followed common sense like this other one « Through two points one can draw only one straight line ». However, after trying to turn it into a theorem[11], mathematicians started wondering what would happen if one supposed it was not true. The now famous 19th century trio Gauss, Bolyai and Lobatchevski independantly worked under the assumption that there could be more than one parallel and created what is now referred to as elliptical geometry. Later that same century, the German Bernhard Riemann decided there could be no parallel at all and his weird assumption gave birth to another kind of geometry, of which our spherical geometry is an example. Indeed, if we accept the idea that the great circles are the only « straight lines » of the sphere then the concept of parallel lines doesn’t exist anymore because two great circles always intersect at two points. Riemann’s work eventually made possible the development of Albert Einstein’s general relativity but that’s a whole nother story and travelling in the high spheres of the geometry of the end of the 19th century requires a level of abstraction which goes beyond the modest ambition of this chronicle.
[1] Yes, numbers have this effect on me, especially when they are given in the metric and the US system.
[2] When asked by Russell what the tortoise was standing on, the lady replied “It’s turtles all the way down”.
[3] « Roughly » because it is slightly flatenned at the poles.
[4] You might think the angle could be more than 90° if you move further than the pole but since you can start from any point on the equator an angle of let’s say 100° would be 80° starting from the other side.
[5] Same as New York City’s streets and avenues.
[6] http://en.wikipedia.org/wiki/International_Meridian_Conference
[7] The pebble eater, remember ?
[8] You may have seen the 1979 movie The China Syndrome, starring Jack Lemmon, Jane Fonda and Michael Douglas.
[9] Is that even a word ? I mean lengthy is already too long so can it be longer than too long ?
[10] Often considered the “father of geography” Eratosthenes measured a little bit more than 7 degrees of latitude along the meridian going through Alexandria and Syena and calculated a measure of earth’s circumference with a an error of only 0.16%.
[11] A postulate or axiom is a statement admitted as self evident and true whereas a theorem is proven using the axioms.
About the Author :
Originally from Brittany, David Soquet graduated from the Université de Rennes, before becoming a math teacher. After honing his skills at a middle school near Paris, he joined the Lycée Français in 2008. He is the father of two children and is passionate about the history of science. In his teaching, he tries to balance the rigor required by mathematics with humor and discovery. He is very curious and his interests range from modular origami and norse mythology to Fritz Lang’s cinema and music.