Pythagoras was the Tom Thumb of Ancient Greece. Wherever he was going, the mathematician was carrying pebbles in his pockets, small stones. The reason is that Pythagoras liked to do calculations, a word that comes from the Latin calculus and literally means “stone”. A kidney stone is called a “calcul” in French and even mathematicians don’t like those. Calculus is also the root in “calculovorus” a furry animal about the size of a rabbit who is feeding on rocks in the ground and is more commonly known as the pebble eater. It’s really too bad it is not endemic in Brittany because I could really have used one when I had to remove the stones from my parents’ garden, certainly the chore I hated the most as a kid[1]. But it’s a bit early for a digression.
The School of Athens, by Raphael. Pythagoras is represented siting in the foreground on the left, writing a book.
Yes, whether he was sunbathing on the beaches of Samos[2] or strolling past the pyramids in Giza, Pythagoras would have pebbles handy. He would sit for hours on the sand and draw shapes with his small stones. First, he drew squares. That was easy enough. He would start with one single stone and then add three more stones to form a 2 by 2 square, then a 3 by 3 square…eventually getting the sequence of numbers 1 4 9 16 25 36 which are called « square numbers ». And maybe because of the way he had successively built his squares, Pythagoras noticed that the number of stones he needed to add at each step also followed a particular sequence : 1 3 5 7 9 11 , the sequence of consecutive odd numbers.
Written in stone
Numbers can be very abstract at times but when written in stone (pun intended) they help visualize this first result : the sum of the first N odd numbers is the square of N.[3] Two comments need to be made about this result. First, mathematicians would not write it as I did. They would use a formula. But to be able to read that formula, we need to understand the difference between value and rank because we need to know the value of the Nth odd number. As we saw, the 6th odd number is 11 and it is quite easy to see that the Nth is 2N-1. That would give us the formula : 1+3+5+…+(2N-1)=N^2.
Secondly, as much as the concrete visualization helped to find the formula, experts would say it is not an exact proof. How do we know that the result will remain true when numbers get bigger ? For all odd numbers under 100 (that is for N=50) the sum should be 50^2=2500 and even Pythagoras didn’t have that many pebbles. Well, to prove the result in a more rigorous way[4] we need to use a very efficient tool : mathematical induction.
Mathematical induction
To put it simply, mathematical induction is a bit like Lewis Carroll’s « Jam tomorrow and jam yesterday» rule except that there is also jam today. I rediscovered that rule recently while rereading Through the Looking Glass and with the risk of boring you with another digression it reminded me of a rule my friends and I tried to put in place during our high-school years. It would go something like “Gym tomorrow and gym yesterday but please no gym today”. Not that we were not into sports, we just disliked to do it between 2 periods of math and 2 periods of philosophy.
Anyway, before we get to understand how that can help mathematicians, let’s see how induction works on a simple example. Consider the two following statements :
- If I shave one day of the week, I also shave the day after.
- I shave on Monday.
As you can easily understand, if these two statements are true it means that I shave each day of the week. However, if the first statement is false, then you know only about Monday. And if the second is false it is possible that I spend the whole week without shaving. Yes, if I don’t shave on any day of the week, the first statement is not false, it just doesn’t apply.
So the trick behind induction is that you never prove that a statement is true for each step, instead you prove that it is true for the first step AND that if it is true for any step it is also true for the following one.
We’re now ready to go back to our result : the sum of the first N odd numbers is the square of N.
Obviously, the statement is true for N=1 as the square of 1 is 1[5].
Now suppose that there is one integer P for which the statement is true, namely that the sum of the first P odd integers is the square of P, or as we saw earlier : 1+3+5+…+(2P-1)=P^2.
The integer after 2P-1 is 2P which is even so the next odd number is 2P+1. If we add it up to the rest we get 1+3+5+…+(2P-1)+(2P+1) or P^2 + (2P+1) according to our supposition. But P^2+2P+1 is the same as (P+1)^2[6] and that means that 1+3+5+…+(2P-1)+(2P+1)=(P+1)^2. In other words, the statement is true for the integer P+1.
We can conclude. We proved that the statement is true for N=1 and we proved that if it is true for one particular integer it is also true for the next. Following the principle of mathematical induction, this proves that the statement is true for all integers. Observation led to conjecture and induction brought the proof.
Tetractys
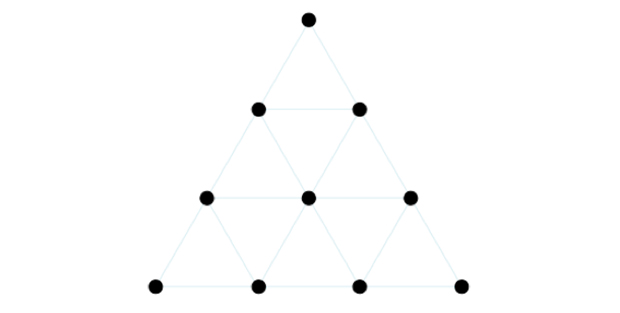
Back to Samos. When he was done with squares, Pythagoras started arranging his pebbles in triangles. Again he started with 1 stone, then added 2 stones under to make an equilateral[7] triangle with 2 stones on each side. Three more stones made another triangle with a side of 3 stones. Finally, Pythagoras made another line with 4 stones and this brought the total to 10, the fourth triangular number.
This number had a lot of significance for Pythagoras, who called it Tetractys. It symbolized the four elements and the four dimensions. His disciples (the so-called Pythagoreans) actually had to take an oath on and pray to the Tetractys. But if one thing is sure, it is that I have no intention to bring mysticism and numerology into this. Instead, let’s see what happens if we increase the triangle by adding more lines at the bottom. The next triangular numbers are 15, 21, 28, 36 and 45 which is the sum of our 10 digits. This naturally brings a question : is it possible to find the value of the Nth triangular numbers without adding up all numbers from 1 to N ? The answer is yes (of course) and figuring it out requires observation and a small shift.
Here’s the idea. It is possible to arrange the pebbles to form a L shaped triangle instead of an equilateral triangle. To do that we just need to vertically align the first pebble of each line. This new triangle is a right-angled isosceles triangle with N stones on each side of the right angle or the equivalent of half a square of side N. There you go ! We obviously need N^2 pebbles to form a square of side N so you’re thinking there should be (N^2)/2 for the triangle. Then it means that 1+2+3+…+N= (N^2)/2, here’s the formula ! Not so fast ! For N=4 this formula gives a total of (4^2)/2=8 and it should be 10. Even worse, for N=5 the formula would give 12.5 which is not even a whole number of pebbles.
Triangular numbers
Are we to start cutting pebbles ? Well no… and then yes. We said the right-angled isosceles triangle was equivalent to half a square because we cut the square through one of its diagonal. This is not a problem with a real geometrical square but if we cut a square of pebbles through the diagonal, we actually cut in half the pebbles on the diagonal. Now if the square has N pebbles on the side it also has N pebbles on the diagonal (right ?)[8] and it means we lost N/2 pebbles[9]. In other words, our formula should be (N^2)/2+N/2 which can also be written as N(N+1)/2. This last version assures that we will always get a whole number of pebbles because whatever the value of N, either N or N+1 is an even number[10]. Let’s check that new formula. For N=9 we get 9*10/2=45 which is indeed the number we found before. Of course, a more rigorous proof would require the use of mathematical induction but the result stands : the sum of all integers from 1 to N is N(N+1)/2.
What I like with triangular numbers is that they are very easy to understand but also give some fun results. As an example, it’s quite easy to see that the sum of two triangular numbers is a square number : 15+21=36=6^2, 21+36=49=7^2 etc… It is simply proven with a clever arrangement of pebbles or some factorization.[11]
Handshakes
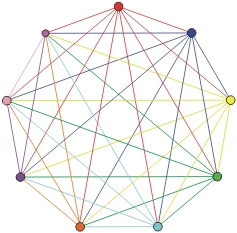
Triangular numbers also give the answer to the famous “handshakes” problem.
Ten persons meet in a room and each one shakes everyone else’s hand. How many handshakes will be necessary ?
100 as is 10*10 is not the right answer because a person does not shake his own hand, nor is 90 because when A shakes B’s hand, B also shakes A’s hand. In the end, we get 10*9/2 = 45 handshakes, the 9th triangular number.
Visualization of the handshakes problem.
And to follow Pythagoras’ steps again, the next arrangements of stones to consider are tridimensional ones which will give us pyramidal numbers. I will consider two kinds, one where the base of the pyramid is a square and one where it is an equilateral triangle. How many pebbles do we need to build them ?
It’s quite simple actually. We just need to add each layer. For the squared base we get 1+4+9+16+…+N^2 , the sum of the first consecutive square numbers, and with mathematical induction it is not so hard to prove that that number equals N(N+1)(2N+1)/6. And if the base is a triangle, the pyramid is also called a tetrahedra and the number of pebbles is the sum of consecutive triangular numbers 1+3+6+10+… N(N+1)/2 which is N(N+1)(N+2)/6. In other words, if you wish to build a 10 stories high pyramid, you would need 220 pebbles for the triangular one and 385 for the square one. And with that many pebbles you should be able to find your way home after this long journey…
[1] As a general rule I disliked chores where I couldn’t see any real progress with time and I remember arguing with my dad and trying to increase the size below which a stone could remain in the soil without bothering potatoes.
[2] A Greek island off the coast of Turkey and the birth place of Pythagoras.
[3] As an example, adding the first 10 odd numbers 1+3+5+7+9+11+13+15+17+19=100 a result you should be able to verify easily by cleverly rearranging the numbers.
[4] Which means in a more Greek axiomatic way.
[5] I know, I know if there is only one number there is no sum per se. Yet another reason why mathematicians use formulas rather than sentences.
[6] Remember (a+b)^2=a^2+b^2+2ab.
[7] An equilateral triangle has three equal sides. An isosceles triangle has two.
[8] Which doesn’t mean the diagonal is as long as the side.
[9] If cutting pebbles bothers you you can also take two identical L shaped triangles of pebbles and turn one of them upside down to form a N by N+1 rectangle.
[10] If N is odd then N+1 is even and the product is even.
[11] Using the formula, the sum of the Nth and the (N+1)th givers N(N+1)/2 + (N+1)(N+2)/2 = (N+1)(N+N+2)/2 = (N+1)(2N+2)/2 = (N+1)(N+1) = (N+1)^2
About the Author :
Originally from Brittany, David Soquet graduated from the Université de Rennes, before becoming a math teacher. After honing his skills at a middle school near Paris, he joined the Lycée Français in 2008. He is the father of two children and is passionate about the history of science. In his teaching, he tries to balance the rigor required by mathematics with humor and discovery. He is very curious and his interests range from modular origami and norse mythology to Fritz Lang’s cinema and music.